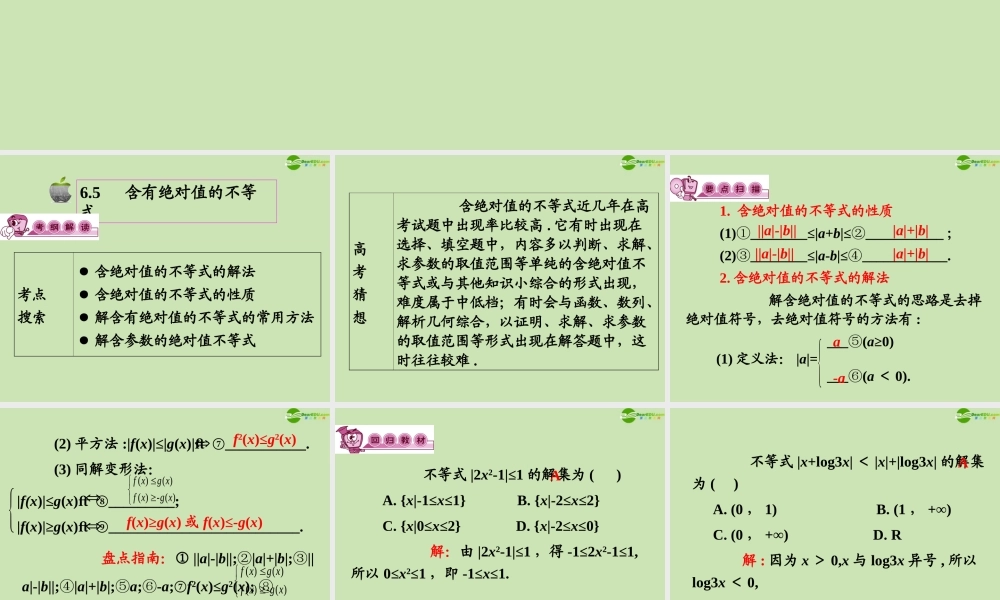
第六章不等式6.5 含有绝对值的不等式 考点搜索● 含绝对值的不等式的解法● 含绝对值的不等式的性质● 解含有绝对值的不等式的常用方法● 解含参数的绝对值不等式高考猜想 含绝对值的不等式近几年在高考试题中出现率比较高 . 它有时出现在选择、填空题中,内容多以判断、求解、求参数的取值范围等单纯的含绝对值不等式或与其他知识小综合的形式出现,难度属于中低档;有时会与函数、数列、解析几何综合,以证明、求解、求参数的取值范围等形式出现在解答题中,这时往往较难 . 1. 含绝对值的不等式的性质 (1)________≤|①a+b|≤___________②; (2)________≤|③a-b|≤____________.④ 2. 含绝对值的不等式的解法 解含绝对值的不等式的思路是去掉绝对值符号,去绝对值符号的方法有 : ___(⑤ a≥0) (1) 定义法: |a|= ___(⑥ a < 0).||a|-|b|||a|+|b|||a|-|b|||a|+|b|a-a (2) 平方法 :|f(x)|≤|g(x)| ___________. ⑦ (3) 同解变形法: |f(x)|≤g(x) _________; ⑧ |f(x)|≥g(x) __________________________. ⑨ 盘点指南:① ||a|-|b||;|② a|+|b|;||③a|-|b||;|④ a|+|b|;⑤a;-⑥ a;⑦f2(x)≤g2(x); ⑧ ;⑨f(x)≥g(x) 或 f(x)≤-g(x) .f2(x)≤g2(x)( )( ) ( )- ( )f xg xf xg x( )( ) ( )- ( )f xg xf xg xf(x)≥g(x) 或 f(x)≤-g(x) 不等式 |2x2-1|≤1 的解集为 ( ) A. {x|-1≤x≤1} B. {x|-2≤x≤2} C. {x|0≤x≤2} D. {x|-2≤x≤0} 解:由 |2x2-1|≤1 ,得 -1≤2x2-1≤1,所以 0≤x2≤1 ,即 -1≤x≤1.A 不等式 |x+log3x| < |x|+|log3x| 的解集为 ( ) A. (0 , 1) B. (1 , +∞) C. (0 , +∞) D. R 解 : 因为 x > 0,x 与 log3x 异号 , 所以log3x < 0, 所以 0 < x < 1.A 已知不等式 |2x-t|+t-1 < 0 的解集为 (- , ) ,则 ______. 解:依题意 |2x-t| < 1-t ,所以t-1 < 2x-t < 1-t , 即 2t-1 < 2x < 1 ,即 t- <x < , 所以 t=0.12121212 1. 设 f(x)= -x ,已知 |x-a| < 1 ,比较 |f(x)-f(a)| 与 2|a|+2 的大小 . 解:因为 f(x)-f(a)=(x-a)(x+a-1) , 所以 |f(x)-f(a)|=|x-a||x+a-1| ≤|x+a-1|=|x-a+2a-1| ≤|x-a|+2|a|+1 < 2|a|+2.题型 1 比较含绝对值的代数式的大小 点评:绝对值不...