余弦函数图像与性质VIP免费

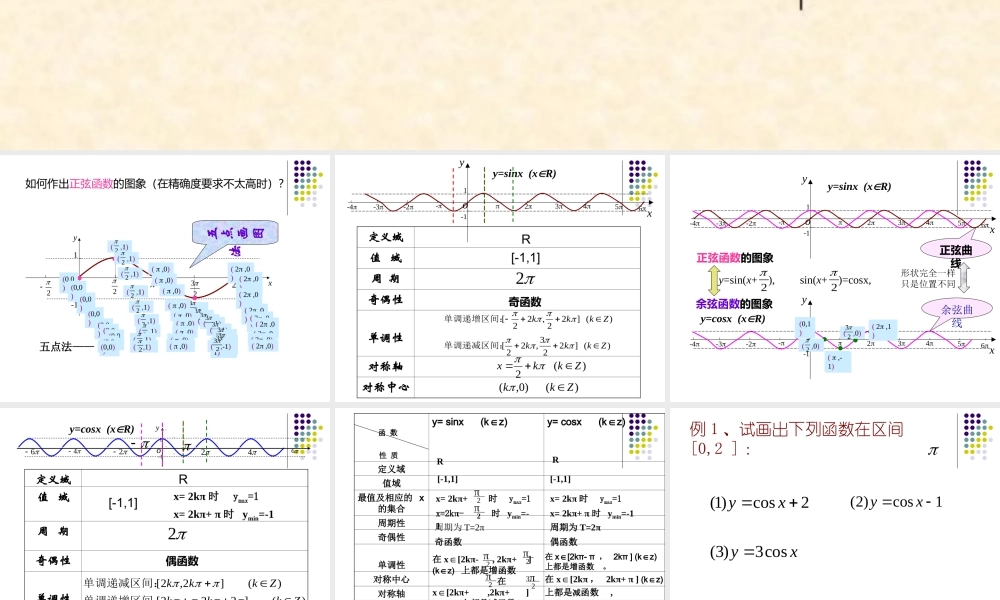
yxo1-122322如何作出正弦函数的图象（在精确度要求不太高时）？(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)五点画图法五点法——(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)定义域值 域周 期奇偶性单调性对称轴对称中心R[-1,1]2)(]223,22[)(]22,22[ZkkkZkkk单调递减区间：单调递增区间：)(2Zkkx)()0,(Zkk奇函数y=sinx (xR) x6yo--12345-2-3-41x6yo--12345-2-3-41余弦函数的图象 正弦函数的图象 x6yo--12345-2-3-41y=sin(x+ ), 2余弦曲线(0,1)( ,0)2(  ,-1)( ,0)23( 2 ,1)正弦曲线形状完全一样只是位置不同(0,1)( ,0)2(  ,-1)( ,0)23( 2 ,1)y=sinx (xR) y=cosx (xR) sin(x+ )=cosx, 2y--1-12o46246--定义域值 域周 期奇偶性单调性对称轴对称中心R[-1,1]2)(]22,2[)(]2,2[ZkkkZkkk单调递增区间：单调递减区间：)(Zkkx )()0,2(Zkk 偶函数 y=cosx (xR) x= 2kπ 时 ymax=1x= 2kπ+ π 时 ymin=-1 函 数 性 质y= sinx (kz)∈y= cosx (kz)∈定义域值域最值及相应的 x的集合周期性奇偶性单调性对称中心对称轴 R R[-1,1][-1,1]x= 2kπ 时 ymax=1x= 2kπ+ π 时 ymin=-1周期为 T=2π周期为 T=2π奇函数偶函数在 x[2kπ- π ∈， 2kπ ] (kz)∈上都是增函数 。在 x[2kπ∈， 2kπ+ π ] (kz)∈上都是减函数 , (kπ,0)x = kπx= 2kπ+ 时 ymax=1x=2kπ- 时 ymin=-1π2π2在 x[2kπ- , 2kπ+ ] ∈(kz) ∈上都是增函数 在x[2kπ+∈ ,2kπ+ ] (kz) ∈上都是减函数 .π2π2π23π2(kπ+ ,0)π2x = kπ+ π2例 1 、试画出下列函数在区间[0,2 ] ：2cos)1(xy1cos)2(xyxycos3)3(例 2 、求下列函数的最大值和最小值以及 相应的 x 值：1cos3)1(xy3)21(cos)2(2 ...