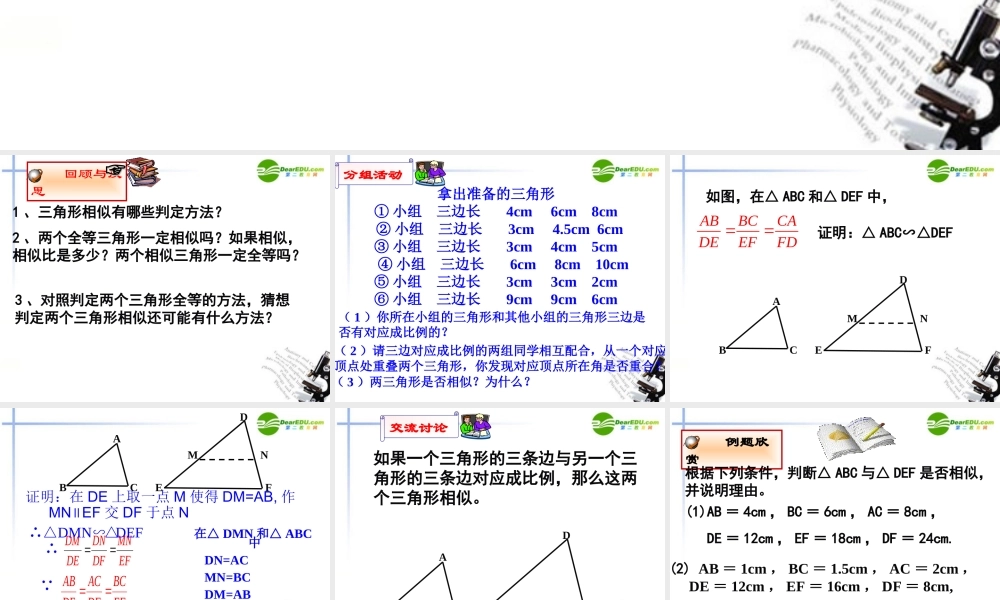
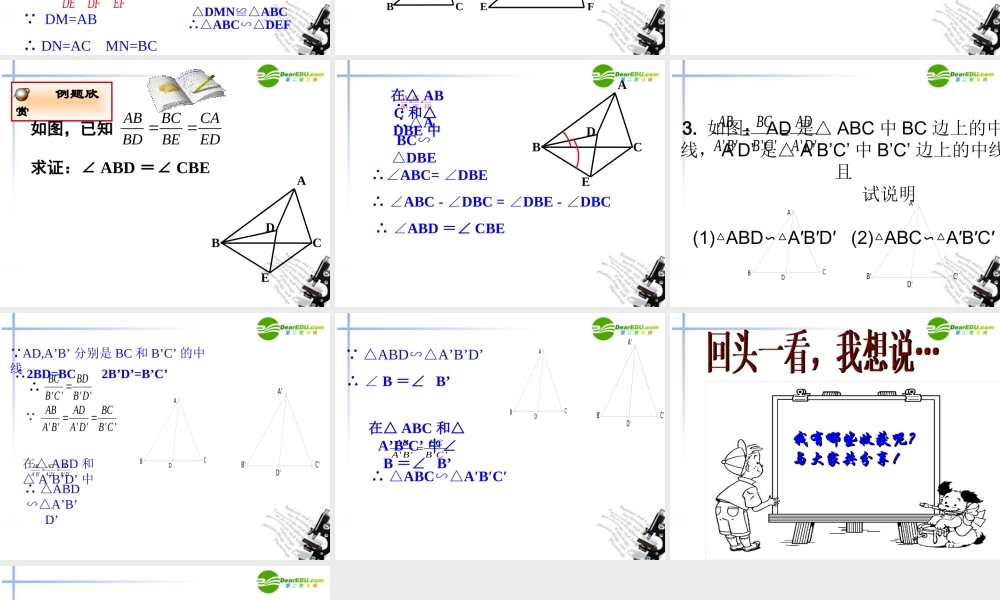
回顾与反思☞☞1 、三角形相似有哪些判定方法?2 、两个全等三角形一定相似吗?如果相似,相似比是多少?两个相似三角形一定全等吗?3 、对照判定两个三角形全等的方法,猜想判定两个三角形相似还可能有什么方法?分组活动拿出准备的三角形① 小组 三边长 4cm 6cm 8cm ② 小组 三边长 3cm 4.5cm 6cm③ 小组 三边长 3cm 4cm 5cm ④ 小组 三边长 6cm 8cm 10cm⑤ 小组 三边长 3cm 3cm 2cm⑥ 小组 三边长 9cm 9cm 6cm( 1 )你所在小组的三角形和其他小组的三角形三边是否有对应成比例的?( 2 )请三边对应成比例的两组同学相互配合,从一个对应顶点处重叠两个三角形,你发现对应顶点所在角是否重合?( 3 )两三角形是否相似?为什么?ABCDEF如图,在△ ABC 和△ DEF 中,证明:△ ABC∽△DEFMNABBCCADEEFFD证明:在 DE 上取一点 M 使得 DM=AB, 作 MN EF∥交 DF 于点 NABCDEFMN ∵ DM=AB ∴ DN=AC MN=BCDMDNMNDEDFEF∴∵ ABACBCDEDFEF∴△DMNDEF∽△在△ DMN 和△ ABC中 DN=AC MN=BC DM=AB △DMNABC≌△∴△ABCDEF∽△交流讨论ABCDEF如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。 例题欣赏根据下列条件,判断△ ABC 与△ DEF 是否相似,并说明理由。(2) AB = 1cm , BC = 1.5cm , AC = 2cm , DE = 12cm , EF = 16cm , DF = 8cm,(1)AB = 4cm , BC = 6cm , AC = 8cm , DE = 12cm , EF = 18cm , DF = 24cm. 例题欣赏如图,已知 ABBCCABDBEED求证:∠ ABD =∠ CBEABCDE∴∠ABC= DBE∠ ∴ ∠ABC - DBC = DBE - DBC∠∠∠ ∴ ∠ABD =∠ CBEABCDE∵ABBCCABDBEED在△ ABC 和△DBE 中∴△ABC∽DBE△3. 如图: AD 是△ ABC 中 BC 边上的中线, A’D’ 是△ A’B’C’ 中 B’C’ 边上的中线,且 试说明(1) ABDA′B′D′ (2) ABCA′B′C△∽△△∽△′A'B'C'D'ABCD' '' '''ABBCADA BB CA D∵AD,A’B’ 分别是 BC 和 B’C’ 的中线' '''' 'ABADBCA BA DB C ∵ 在△ ABD 和△ A’B’D’ 中' '''''ABADBDA BA DB D ∴ △ABDA’B’∽△D’' '''BCBDB CB D∴∴2BD=BC 2B’D’=B’C’A'B'C'D'ABCDA'B'C'D'ABCD ∵ △ABDA’B’D’∽△ ∴ ∠ B =∠ B’''''ABBCA BB C在△ ABC 和△A’B’C’ 中∠ B =∠ B’ ∴ △ABCA′B′C′∽△我有哪些收获呢?我有哪些收获呢?与大家共分享!与大家共分享! 知识像一艘船,让它载着我们驶向理想的 ……再再见见 !!