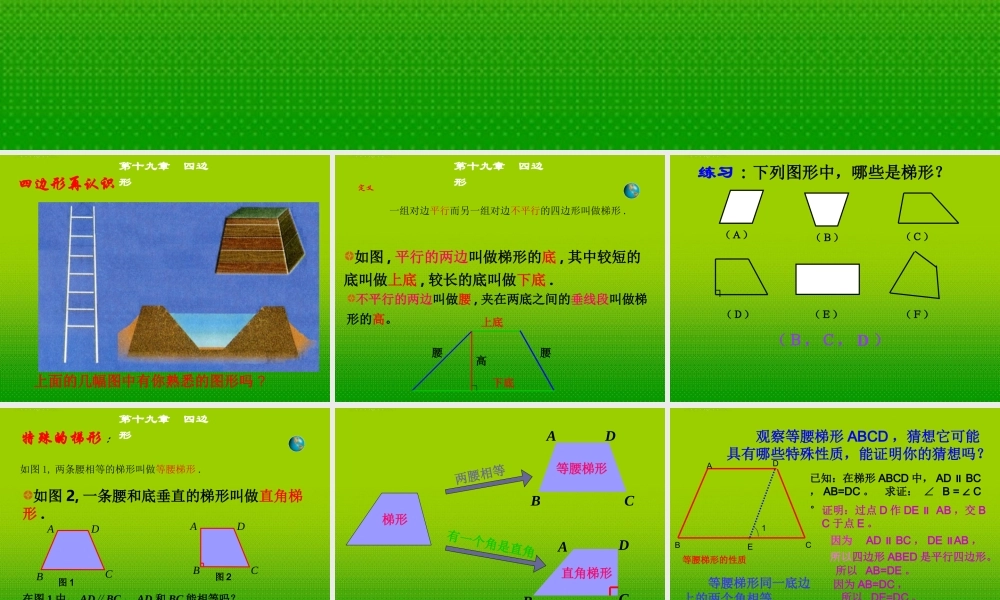
人教版八年级(下册)第十九章四边形19.3 梯形(第 1 课时)上面的几幅图中有你熟悉的图形吗 ?第十九章 四边形四边形再认识定义 一组对边平行而另一组对边不平行的四边形叫做梯形 .上底下底腰腰高不平行的两边叫做腰 , 夹在两底之间的垂线段叫做梯形的高。如图 , 平行的两边叫做梯形的底 , 其中较短的底叫做上底 , 较长的底叫做下底 .第十九章 四边形练习 : 下列图形中,哪些是梯形?(A)(B)(D)(E)(F)(C)(B,C, D )┐如图 1, 两条腰相等的梯形叫做等腰梯形 .特殊的梯形 :如图 2, 一条腰和底垂直的梯形叫做直角梯形 .图 1ABCD图 2ABCD在图 1 中, AD∥BC , AD 和 BC 能相等吗?在图 2 中, AB⊥BC ,那么, AB⊥AD 吗? AB 叫梯形的高。当 AB ⊥BC 时, CD 也能垂直 BC 吗?第十九章 四边形梯形两腰相等有一个角是直角ABCD等腰梯形ADCB直角梯形 观察等腰梯形 ABCD ,猜想它可能具有哪些特殊性质,能证明你的猜想吗?已知:在梯形 ABCD 中, AD BC∥, AB=DC 。 求证: ∠ B = C∠。A BCDE1等腰梯形的性质 等腰梯形同一底边上的两个角相等。 等腰梯形的对角线相等。证明:过点 D 作 DE AB∥,交 BC 于点 E 。 因为 AD BC∥, DE AB∥, 所以四边形 ABED 是平行四边形。所以 AB=DE 。因为 AB=DC , 所以 DE=DC 。所以∠ 1= C∠。而 ∠ 1= B∠,所以∠ B= C∠。ABDCEF证明:过 A , D 分别作 AE⊥BC ,DF⊥BC ,垂足分别为点 E , F 。因为 AD ∥ BC ,所以四边形 AEFD 是平行四边形。 所以 AE = DF 。因为 AB = DC , 所以∆ ABE≌∆DCF (HL) 。所以∠ B= C∠。 证明方法2因为 AEBC⊥, DFBC⊥,所以 AE ∥ DF 。已知:在梯形 ABCD 中, AD BC∥, AB=DC 。 求证: ∠ B = C∠ABDCO等腰梯形的性质 2 等腰梯形的两条对角线相等。已知:在梯形 ABCD 中, AD BC ,AB = CD ,求证: BD = AC∥所以∠ ABC= DCB∠。证明:在梯形 ABCD 中,因为 AB = DC ,因为 BC=CB ,所以△ ABCDCB.≌△ 所以 AC = BD.AB梯形 ABCD,AD BC,AB=CD∥DC等腰梯形的性质1 、等腰梯形同一底边上的两个底角相等2 、等腰梯形的两条对角线相等3 、等腰梯形是轴对称图形,上下底的中点连线所在直线是对称轴 例 1 :如图,延长等腰梯形 ABCD 腰 BA ...