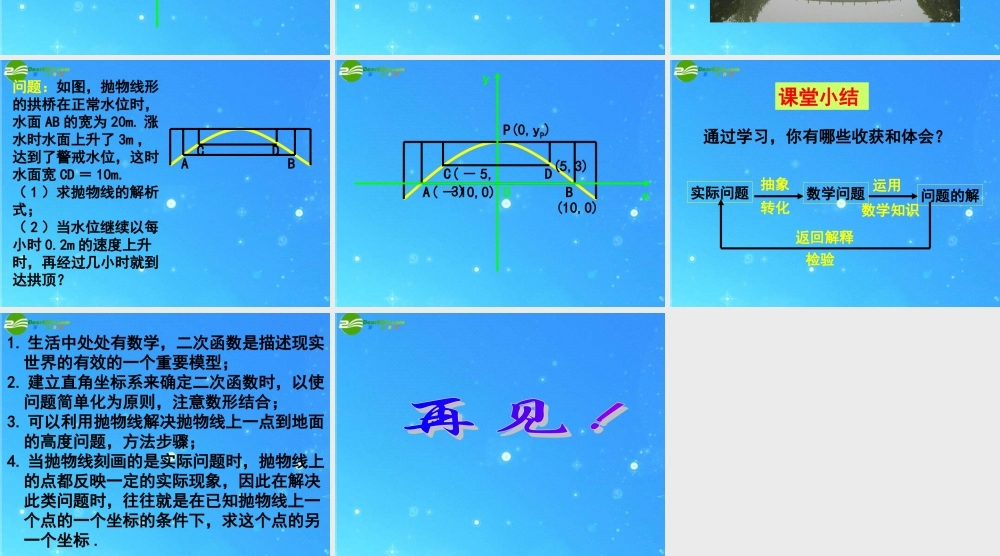
喷泉 (1) 问题:如图,人工喷泉有一个竖直的喷水枪 AB ,喷水口 A 距地面 2m ,喷水水流的轨迹是抛物线 . 如果要求水流的最高点 P 到喷水枪 AB 所在直线的距离为 1m ,且水流的着地点 C 距离水枪底部 B 的距离为 2.5 m ,那么,水流的最高点距离地面是多少米? ABCP ABCP(0,2)(2.5,0)(1,yp )( 0,0 ) Oxy ABCP( - 1,2)(1.5,0)(0,yp )(- 1,0 )Oxy 方法步骤:① 恰当建立直角坐标系;② 求出抛物线的解析式;③ 把抛物线上顶点的横坐标代入解析式,求出顶点的纵坐标;④ 顶点的纵坐标的绝对值即为最值 . 问题:如图,抛物线形的拱桥在正常水位时,水面 AB 的宽为 20m. 涨水时水面上升了 3m ,达到了警戒水位,这时水面宽 CD = 10m.( 1 )求抛物线的解析式;( 2 )当水位继续以每小时 0.2m 的速度上升时,再经过几小时就到达拱顶?ABCD xyABCDO( - 10,0)(10,0)( - 5,3)(5,3)P(0,yP) 实际问题 抽象转化数学问题 运用数学知识问题的解返回解释检验课堂小结通过学习,你有哪些收获和体会? 1. 生活中处处有数学,二次函数是描述现实世界的有效的一个重要模型;2. 建立直角坐标系来确定二次函数时,以使问题简单化为原则,注意数形结合;3. 可以利用抛物线解决抛物线上一点到地面的高度问题,方法步骤;4. 当抛物线刻画的是实际问题时,抛物线上的点都反映一定的实际现象,因此在解决此类问题时,往往就是在已知抛物线上一个点的一个坐标的条件下,求这个点的另一个坐标 .