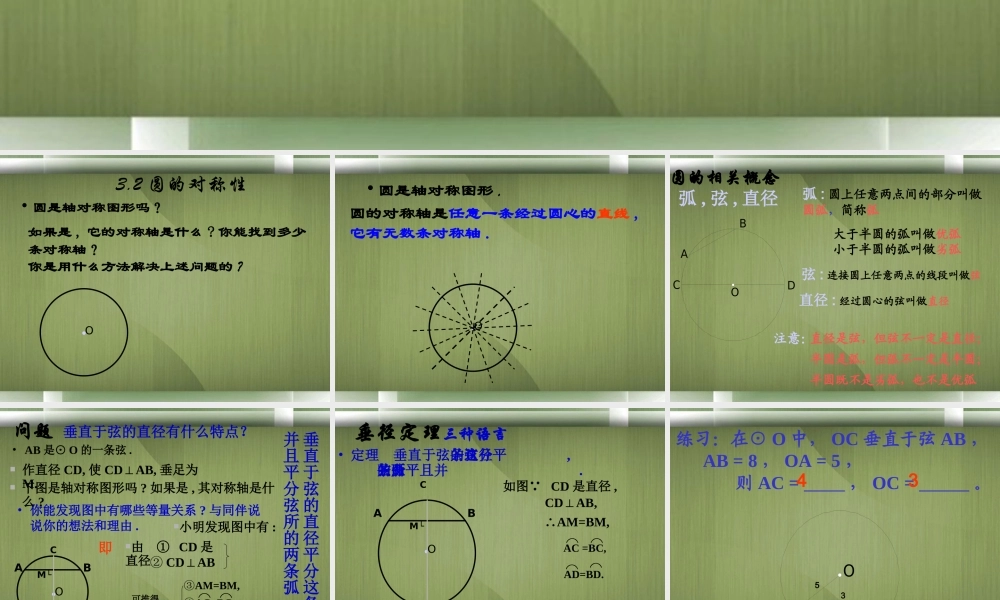
九年级数学 ( 下 ) 第三章 圆3.2 圆的对称性 ( 第一课时 )3.2 圆的对称性• 圆是轴对称图形吗?如果是 , 它的对称轴是什么 ? 你能找到多少条对称轴?●O你是用什么方法解决上述问题的 ?• 圆是轴对称图形 .圆的对称轴是任意一条经过圆心的直线 ,它有无数条对称轴 .●OABCDO弧 : 圆上任意两点间的部分叫做圆弧,简称弧大于半圆的弧叫做优弧小于半圆的弧叫做劣弧 弦 : 连接圆上任意两点的线段叫做弦 直径 : 经过圆心的弦叫做直径 直径是弦,但弦不一定是直径;半圆是弧,但弧不一定是半圆;半圆既不是劣弧,也不是优弧 注意:圆的相关概念 弧 , 弦 , 直径③AM=BM,问题 垂直于弦的直径有什么特点? • AB 是⊙ O 的一条弦 .• 你能发现图中有哪些等量关系 ? 与同伴说说你的想法和理由 . 作直径 CD, 使 CDAB,⊥垂足为M.●O 下图是轴对称图形吗 ? 如果是 , 其对称轴是什么 ?小明发现图中有 :ABCDM└由 ① CD 是直径 ② CDAB⊥可推得⌒ ⌒④AC=BC,⌒ ⌒⑤AD=BD.即垂直于弦的直径平分这条弦,并且平分弦所的两条弧.垂径定理三种语言• 定理 垂直于弦的直径平分这条弦, 并且平分弦所的两条弧.ABCD●OM└CDAB,⊥如图 CD 是直径 ,∴AM=BM,⌒ ⌒ AC =BC,⌒ ⌒ AD=BD.练习:在⊙ O 中, OC 垂直于弦 AB , AB = 8 , OA = 5 , 则 AC = , OC = 。ABCO┏584343②CDAB,⊥问题 平分弦的直径有什么特点?• AB 是⊙ O 的一条弦 , 且 AM=BM.• 你能发现图中有哪些等量关系 ? 与同伴说说你的想法和理由 .过点 M 作直径 CD.●O下图是轴对称图形吗 ? 如果是 , 其对称轴是什么 ?小明发现图中有 :CD由 ① CD 是直径 ③ AM=BM可推得⌒ ⌒④AC=BC,⌒ ⌒⑤AD=BD.● AB┗平分弦的直径垂直于弦, 并且平 分弦所对的两条弧 .平分弦( 不是直径 ) 的直径垂直于弦 , 并且平分弦所对的两条弧.M垂径定理的逆定理三种语言●OABCD∴ CDAB,⊥如图 CD 是直径AM=BM⌒ ⌒ AC =BC,⌒ ⌒ AD=BD.平分弦(不是直径)的直径垂直于弦 ,并且平分弦所对的两条弧.M例 1 如图,一条公路的转弯处是一段圆弧(即图中弧 CD, 点 0 是弧 CD 的圆心),其中CD=600m , E 为弧 CD 上的一点,且 OE 垂直于 CD ,垂足为 F , EF=90m. 求这段弯路的半径。EODCF1. 已知:如图,在以 O为圆心的两个同心圆中,大圆的弦 AB...