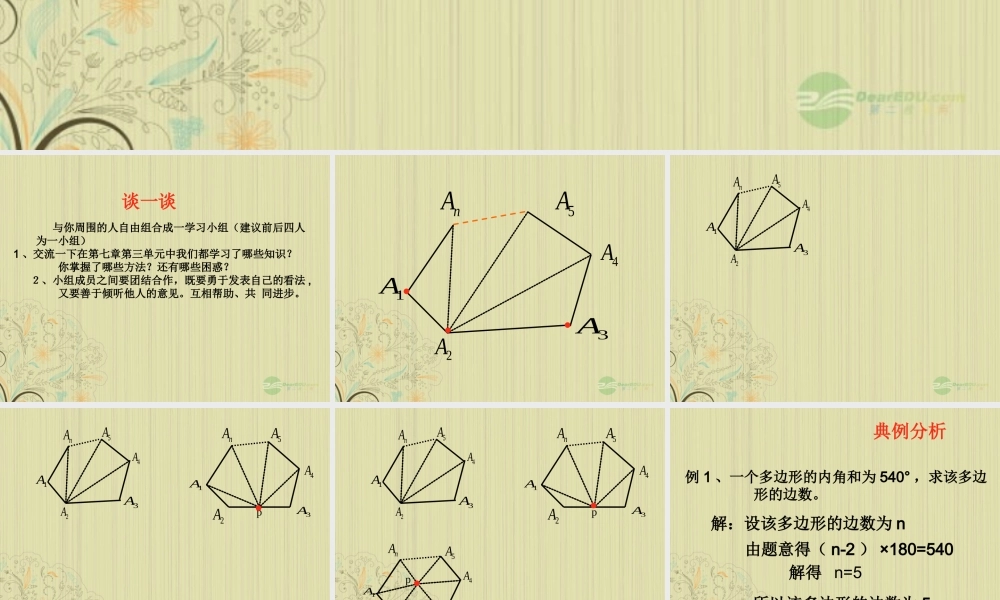
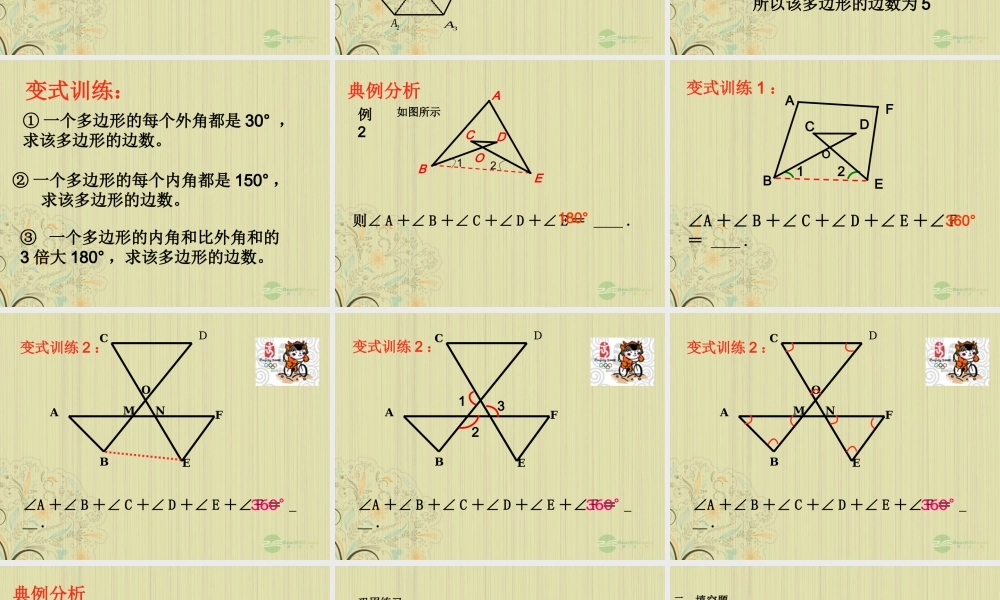
7.3 多边形及其内角和谈一谈 与你周围的人自由组合成一学习小组(建议前后四人 为一小组) 1 、交流一下在第七章第三单元中我们都学习了哪些知识? 你掌握了哪些方法?还有哪些困惑? 2、小组成员之间要团结合作,既要勇于发表自己的看法 , 又要善于倾听他人的意见。互相帮助、共 同进步。2A3A1A4A5AnA2A3A1A4A5AnA2A3A1A4A5AnA2A1A3A4A5AnAp2A3A1A4A5AnA1A4A3A2A5AnAp2A1A3A4A5AnAp 典例分析例 1 、一个多边形的内角和为 540° ,求该多边 形的边数。 解:设该多边形的边数为 n由题意得( n-2 ) ×180=540解得 n=5所以该多边形的边数为 5② 一个多边形的每个内角都是 150° , 求该多边形的边数。① 一个多边形的每个外角都是 30° ,求该多边形的边数。③ 一个多边形的内角和比外角和的3 倍大 180° ,求该多边形的边数。变式训练:则∠ A +∠ B +∠ C +∠ D +∠ E = .180°典例分析例212如图所示OEDCBA∠A +∠ B +∠ C +∠ D +∠ E +∠ F= .360°变式训练 1 :21OFECDBA∠A +∠ B +∠ C +∠ D +∠ E +∠ F = .DBEAFC360°变式训练 2 :MNO∠A +∠ B +∠ C +∠ D +∠ E +∠ F = .DBEAFC360°变式训练 2 :123∠A +∠ B +∠ C +∠ D +∠ E +∠ F = .DBEAFC360°变式训练 2 :MNO例 3 、典例分析小明在广场上散步,他从 A 点出发前进 10 米,向右转 15 ° ,再前进 10 米,又向右转 15 ° ,……这样一直走下去,他第一次回到出发点 A 时,一共走了多少米?15 °15 °分析:由题意知,小明散步的路线恰好是一个正多边形,他第一次回到出发点 A 时,所走的路程就是该正多边形的的周长。由于该正多边形的边长为 10 米,所以只要借助外角求出其边数,即可解决问题。A 巩固练习:一、选择题:1 、下列说法不正确的是( ) A 、正多边形的各边都相等 B 、各边都相等的多边形是正多边形 C 、正三角形就是等边三角形 D 、各内角都相等的多边形不一定是正多边形2 、若从一个多边形的一个顶点出发,最多可引 8 条对角线, 则它是( ) A 、十一边形 B 、十边形 C 、九边形 D 、八边形3 、一个 n 边形的内角和与外角和的比是 4:1 ,则 n 的值是( ) A 、 10 B 、 6 C 、 7 D 、 84 、一个多边形的边数每增加 1 ,它的内角和与外角和( ) A...