数学 第四章 导数应用 4.1.1 导数与函数的单调性课件 北师大版选修1 1 课件VIP免费

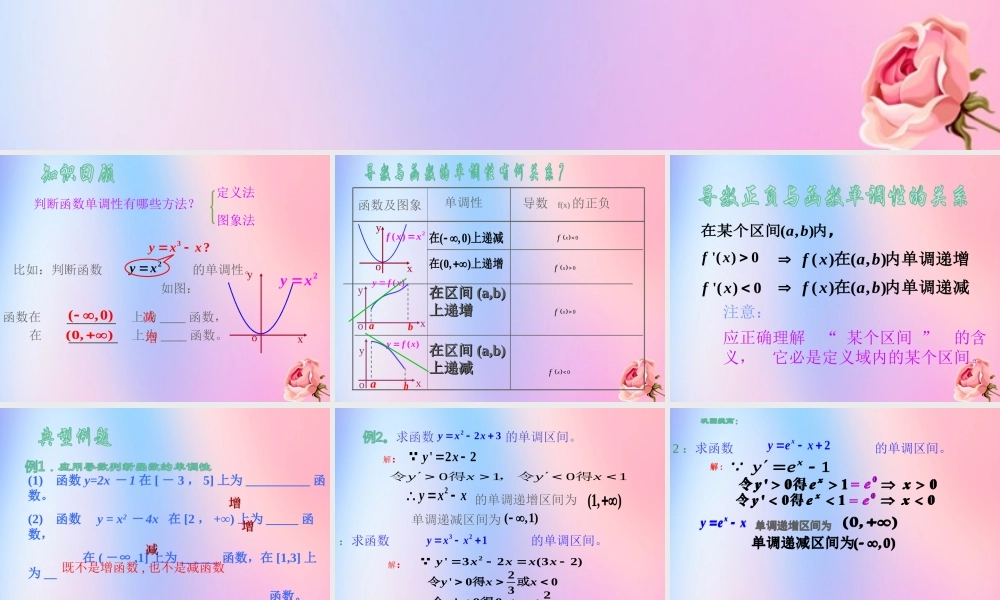
判断函数单调性有哪些方法？比如：判断函数 的单调性。yx2 (,0)(0,)3?yxxxyo2yx函数在 上为 ____ 函数，在 上为 ____ 函数。图象法定义法减增如图：单调性导数 f(x) 的正负函数及图象 (,0)在上递减(0,)在上递增xyoyf x ( )abxyoyf x ( )abxyo2( )f xx在区间在区间 (a,b)(a,b)上递增上递增在区间在区间 (a,b)(a,b)上递减上递减 '0xf '0xf '0xf '0xfa b( , )在某个区间内,fx '( )0f xa b( )( , )在内单调递增fx '( )0f xa b( )( , )在内单调递减注意：应正确理解 “ 某个区间 ” 的含义， 它必是定义域内的某个区间。(1) 函数 y=2x － 1 在 [ － 3 ， 5] 上为 __________ 函数。 (2) 函数 y = x2 － 4x 在 [2 ， +∞) 上为 _____ 函数， 在 ( －∞ ,1] 上为 ______ 函数，在 [1,3] 上为 __ __________________________________ 函数。增增增增减减既不是增函数 , 也不是减函数变 1 ：求函数 的单调区间。321yxx解：2'32(32)yxxxx2'003yxx令得或2'003yx令得32yxx的单调递增区间为单调递减区间为2(0,)32(,0),(,)3 223yxx2yxx(1,)的单调递增区间为'22yx解：单调递减区间为 (,1) 1010xyxy得，令得令变 2 ：求函数 的单调区间。2xyex解 :(0,)(,0)  单调递减区间为1xeyxyex单调递增区间为 (0,)(,0)  单调递减区间为解 :1xeyxyex单调递增区间为① 求定义域②求'( )fx③ 令'( )0( )'( )0( )fxf xfxf x解不等式的递增区间解不等式的递减区间④ 写出单调区间用“导数法” 求单调区间的步骤：-22-11f x  = x+1xxOy∴y=x+ 的单调减区间是 ( － 1 ， 0) 和 (0 ，1)x1x1x1222)1)(1(1xxxxx y′=(x+ )′=1 － 1·x － 2 = 2)1)(1(xxx令 ＞ 0. 解得 x ＞ 1 或 x ＜－ 1.x1∴y=x+ 的单调增区间是 ( －∞，－ 1) 和 (1 ， +∞).2)1)(1(xxx令 ＜ 0 ，解得－ 1 ＜ x ＜ 0 或 0 ＜ x ＜ 1.Rxxx ,0解：函数的定义域为xyo12( )yf xxyo12( )yf xxyo1 2( )yf xxyo12( )yf xxyo'( )yfx2(A)(B)(C)(D)C( )f x'( )fx'( )yfx( )yf x1. 函数1522xxy的递减区间是（）A. 1,B. ,1C. 1,D.  ,12. 函数13)(23xxxf是减函数的区间为 ()A．),2( B．)2,(C．)0,(D．（0，2）3.求函数的单调性（1）3)(xxxf（2）31232)(23xxxxf（3）)3()(2xxxf