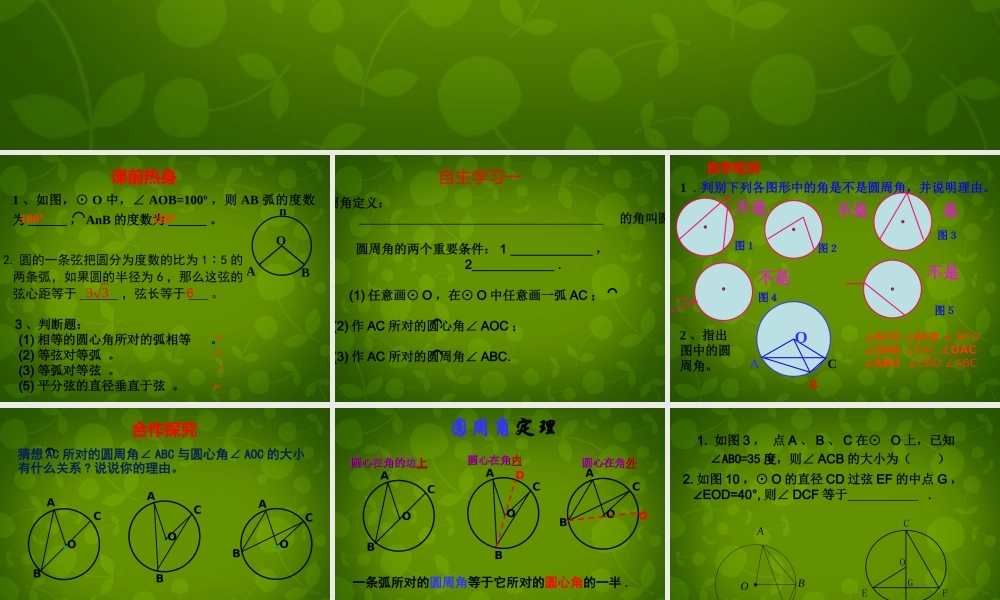
3.3 圆周角和圆心角的关系 (1) 课前热身1 、如图,⊙ O 中,∠ AOB=100º ,则 AB 弧的度数为 ______ , AnB 的度数为 ______ 。AOB n100º260º√×××3 、判断题: (1) 相等的圆心角所对的弧相等 。 (2) 等弦对等弧 。 (3) 等弧对等弦 。 (5) 平分弦的直径垂直于弦 。⌒ 2. 圆的一条弦把圆分为度数的比为 1∶5 的 两条弧,如果圆的半径为 6 ,那么这弦的 弦心距等于 ______ ,弦长等于 ___ 。3 36自主学习一(一)圆周角定义: 的角叫圆周角 . 圆周角的两个重要条件: 1 , 2 .(二) (1) 任意画⊙ O ,在⊙ O 中任意画一弧 AC ; (2) 作 AC 所对的圆心角∠ AOC ; (3) 作 AC 所对的圆周角∠ ABC.⌒⌒⌒自学检测1 、判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图52 、指出图中的圆周角。AOBC∠ACO ∠ACB ∠ BCO ∠OAB ∠BAC ∠OAC ∠ABO ∠CBO ∠ABC猜想 AC 所对的圆周角∠ ABC 与圆心角∠ AOC 的大小有什么关系 ? 说说你的理由。提示 : 注意圆心与圆周角的位置关系 .ABC●OABC●O●OABC合作探究⌒圆周角定理提示 : 圆周角定理是承上启下的知识点 , 要予以重视 .●OABC●OABC●OABCDD圆心在角的边圆心在角的边上上圆心在角圆心在角外外圆心在角圆心在角内内一条弧所对的圆周角等于它所对的圆心角的一半 . 1. 如图 3 , 点 A 、 B 、 C 在⊙ O 上,已知 ∠ABO=35 度,则∠ ACB 的大小为( ) ABCO图 32. 如图 10 ,⊙ O 的直径 CD 过弦 EF 的中点 G , ∠EOD=40°, 则∠ DCF 等于 .OCFGDE图 10例 1. 如图: OA 、 OB 、 OC 都是⊙ O 的半径 ∠ AOB=2BOC. ∠求证:∠ ACB=2BAC.∠∠AOB=2BOC∠AOBC∠ACB=2BAC∠证明: 规律 : 解决圆周角和圆心角的计算和证明问题 , 要准确找出同弧所对的圆周角和圆心角 , 然后再灵活运用圆周角定理 ⌒分析 :AB 所对圆周角是∠ ACB, 圆心角是∠ AOB. 则∠ACB= AOB. BC∠所对圆周角是∠ BAC , 圆心角是∠ BOC, 则∠ BAC= BOC∠ ⌒2121∠ACB= AOB∠21∠BAC= BOC∠21练习:2. 如图,圆心角∠ AOB=100° ,则∠ ACB=___ 。OABCBAO.70°x1. 求圆中角 X 的度数130°AO.X120° C C D B3 、 如图,在直径为 AB 的半圆中, O为圆心, C 、 D 为半圆上的两点,∠ COD=5...