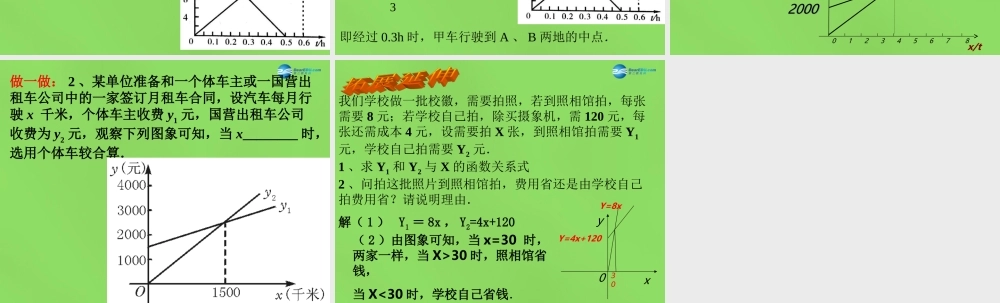
5 一元一次不等式与一次函数 5 一元一次不等式与一次函数 求 ax+b>0 (或 <0 )( a , b是常数, a≠0 )的解集. 求 ax+b>0 (或 <0 )( a , b是常数, a≠0 )的解集.函数 y= ax+b 的函数值大于 0 (或小于 0 )时 x的取值范围.直线 y= ax+b 在 x 轴上方或下方时自变量的取值范围从数的角度看从形的角度看练习:利用函数图象解不等式: 3x - 4 < x+2( 用两种方法 ) .yx0-63Y=2x-6解法 1 :化简不等式得 2x - 6< 0 ,画出函数 y = 2x - 6 的图象.当 x < 3 时 y = 2x - 6 < 0 ,所以不等式的解集为 x < 3 .解法 2 :画出函数 y = 3x- 4 和函数 y = x+2 的图象,交点横坐标为 3 .当 x < 3 时,对于同一个 x ,直线 y = 3x - 4 上的点在直线 y = x+2 上相应点的下方,这表示 3x - 4 < x+2 ,所以不等式的解集为 x < 3 .3yx0y = x + 2y = 3x - 4例:甲、乙两辆摩托车从相距 20km 的 A 、 B 两地相向而图中 l1 、 l2 分别表示两辆摩托车离开 A 地的距离s ( km )与行驶时间 t ( h )之间函数关系.( 1 )哪辆摩托车的速度较快?( 2 )经过多长时间,甲车行驶到 A 、 B 两地中点? 解答:( 1 )从图象中可知hthtkms5.06.020乙甲,, 乙甲乙甲即,,vvhkmvhkmv)/(5.020)/(31006.020故摩托车乙速度快.( 2 )当 s=10km 时,)(3.0310010ht甲 即经过 0.3h 时,甲车行驶到 A 、 B 两地的中点. 做一做: 1 、如图, l1 反映了某产品的销售收入与销售量之间的关系, l2 反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利. ( 1 )根据函数图象写出 l1 、 l2 的函数解析式.( 2 )试分析该产品的盈亏情况.做一做: 1 、如图, l1 反映了某产品的销售收入与销售量之间的关系, l2 反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利. ( 1 )根据函数图象写出 l1 、 l2 的函数解析式.( 2 )试分析该产品的盈亏情况.x/t234567810y/ 元2000200040004000l1l1l2l2做一做: 2 、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶 x 千米,个体车主收费 y1 元,国营出租...