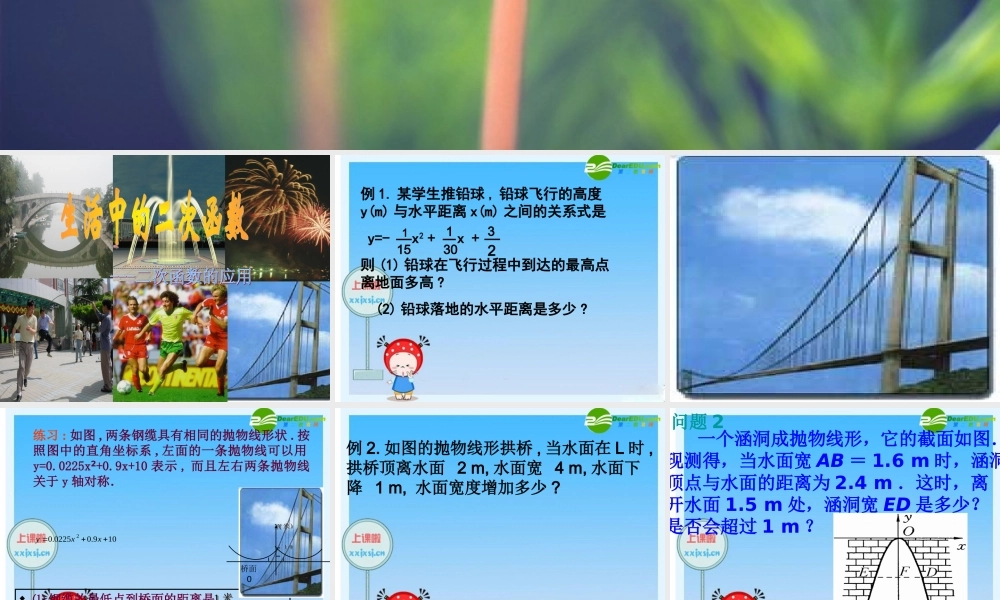
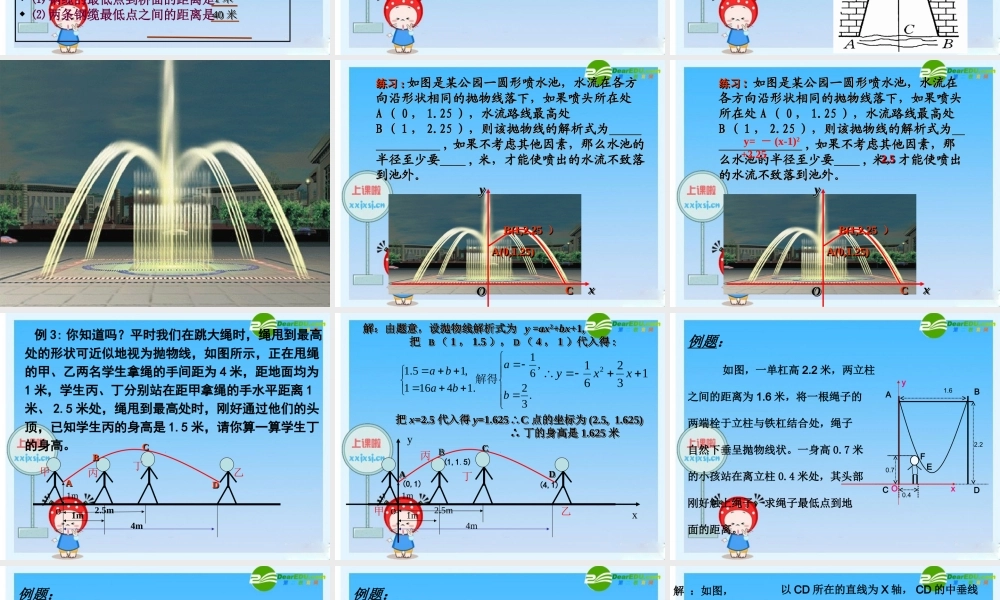
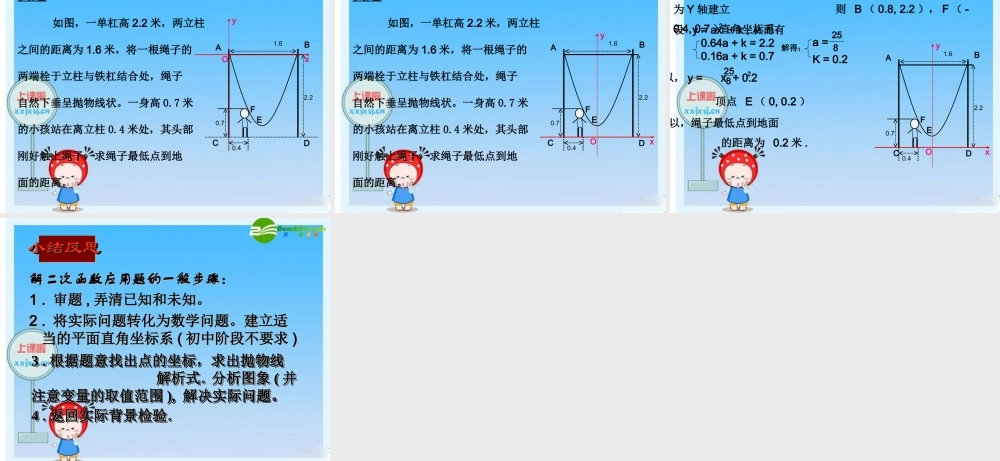
26.3 实际问题与一元二次方程例 1. 某学生推铅球 , 铅球飞行的高度y(m) 与水平距离 x(m) 之间的关系式是 y=- x2 + x + 则 (1) 铅球在飞行过程中到达的最高点离地面多高 ? (2) 铅球落地的水平距离是多少 ?11513032 ⑴ 钢缆的最低点到桥面的距离是 ⑵ 两条钢缆最低点之间的距离是11 米米11 米米4040 米米4040 米米109.00225.02xxy 桥面 0XX(( 米米 ))XX(( 米米 ))Y(Y( 米)米)Y(Y( 米)米) 1010 1010练习 : 如图 , 两条钢缆具有相同的抛物线形状 . 按照图中的直角坐标系 , 左面的一条抛物线可以用y=0.0225x +0.9x+10²表示 , 而且左右两条抛物线关于 y 轴对称. 例 2. 如图的抛物线形拱桥 , 当水面在 L 时 ,拱桥顶离水面 2 m, 水面宽 4 m, 水面下降 1 m, 水面宽度增加多少 ?问题 2 一个涵洞成抛物线形,它的截面如图.现测得,当水面宽 AB = 1.6 m 时,涵洞顶点与水面的距离为 2.4 m .这时,离开水面 1.5 m 处,涵洞宽 ED 是多少?是否会超过 1 m ?练习练习 :: 如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下,如果喷头所在处A ( 0 , 1.25 ),水流路线最高处B ( 1 , 2.25 ),则该抛物线的解析式为 , 如果不考虑其他因素,那么水池的半径至少要 , 米,才能使喷出的水流不致落到池外。练习练习 :: 如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下,如果喷头所在处A ( 0 , 1.25 ),水流路线最高处B ( 1 , 2.25 ),则该抛物线的解析式为 , 如果不考虑其他因素,那么水池的半径至少要 , 米,才能使喷出的水流不致落到池外。 .. ..CCCCxxxxOOOO A(0,1.25)A(0,1.25) A(0,1.25)A(0,1.25) B(1,2.25 B(1,2.25 )) B(1,2.25 B(1,2.25 )) yyyy练习练习 :: 如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下,如果喷头所在处 A ( 0 , 1.25 ),水流路线最高处B ( 1 , 2.25 ),则该抛物线的解析式为 , 如果不考虑其他因素,那么水池的半径至少要 , 米,才能使喷出的水流不致落到池外。练习练习 :: 如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下,如果喷头所在处 A ( 0 , 1.25 ),水流路线最高处B ( 1 , 2.25 ),则该抛物线的解析式为 , 如果不考虑其他因素,那么水池的...