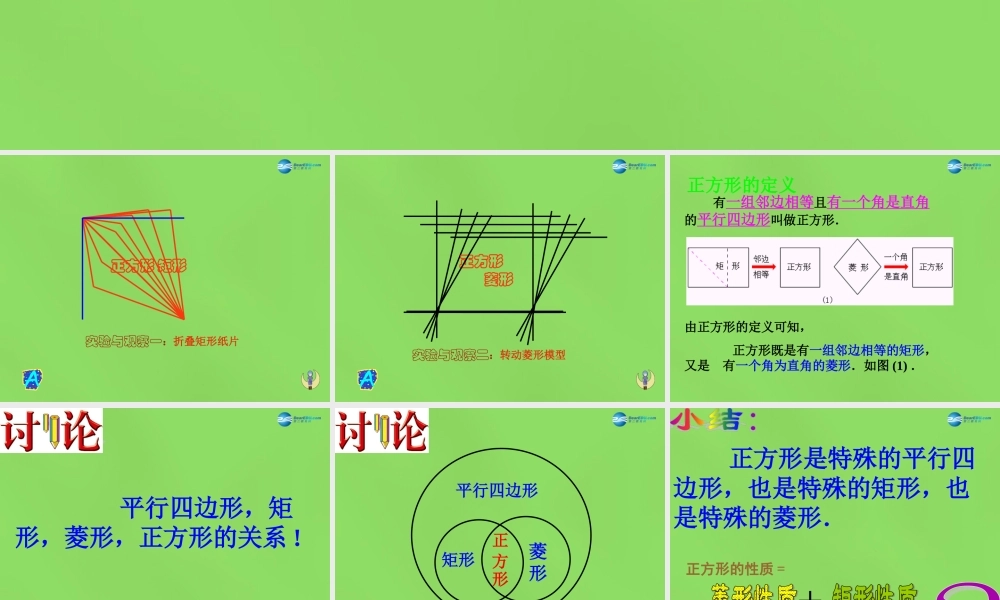
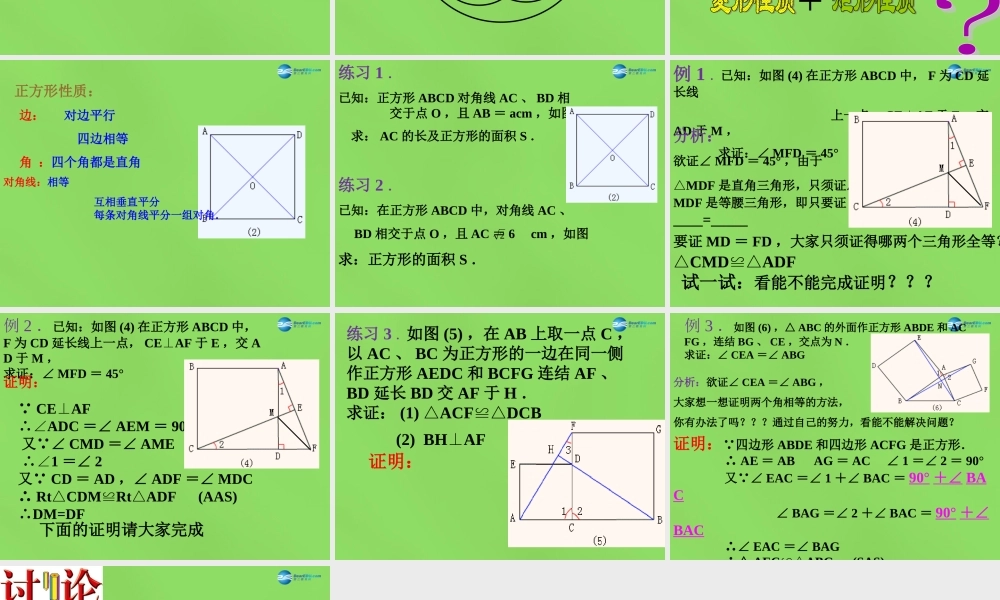
19 . 3 . 3 正方形正方形 矩形实验与观察一:折叠矩形纸片正方形菱形实验与观察二:转动菱形模型 正方形的定义由正方形的定义可知, 正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形.如图 (1) . 有一组邻边相等且有一个角是直角的平行四边形叫做正方形. 平行四边形,矩形,菱形,正方形的关系 !菱形矩形平行四边形正形方 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.正方形的性质 = 正方形性质: 边: 对边平行 四边相等 角 :四个角都是直角对角线:相等 互相垂直平分 每条对角线平分一组对角. 练习 1 .已知:正方形 ABCD 对角线 AC 、 BD 相 交于点 O ,且 AB = acm ,如图 (2) . 求: AC 的长及正方形的面积 S . 练习 2 .已知:在正方形 ABCD 中,对角线 AC 、 BD 相交于点 O ,且 AC = 6 cm ,如图求:正方形的面积 S . 2例 1 .已知:如图 (4) 在正方形 ABCD 中, F 为 CD 延长线 上一点, CEAF⊥于 E ,交AD 于 M , 求证:∠ MFD = 45°分析:欲证∠ MFD = 45° ,由于△MDF 是直角三角形,只须证△MDF 是等腰三角形,即只要证 _____=_____要证 MD = FD ,大家只须证得哪两个三角形全等? 试一试:看能不能完成证明???△CMDADF≌△例 2 .已知:如图 (4) 在正方形 ABCD 中,F 为 CD 延长线上一点, CEAF⊥于 E ,交 AD 于 M ,求证:∠ MFD = 45°证明: ∵ CEAF⊥ ADC∴∠=∠ AEM = 90° 又∵∠ CMD =∠ AME 1∴∠ =∠ 2 又∵ CD = AD ,∠ ADF =∠ MDC ∴ RtCDMRtADF△≌△ (AAS) DM=DF∴ 下面的证明请大家完成练习 3 .如图 (5) ,在 AB 上取一点 C ,以 AC 、 BC 为正方形的一边在同一侧作正方形 AEDC 和 BCFG 连结 AF 、BD 延长 BD 交 AF 于 H .求证: (1) ACFDCB△≌△ (2) BHAF⊥ 证明: 例 3 .如图 (6) ,△ ABC 的外面作正方形 ABDE 和 ACFG ,连结 BG 、 CE ,交点为 N .求证:∠ CEA =∠ ABG 分析:欲证∠ CEA =∠ ABG ,大家想一想证明两个角相等的方法,你有办法了吗???通过自己的努力,看能不能解决问题?证明:∵四边形 ABDE 和四边形 ACFG 是正方形. ∴ AE = AB AG = AC ∠ 1 =∠ 2 = 90° 又∵∠ EAC =∠ 1 +∠ BAC = 90° +∠ BAC ∠ BAG =∠ 2 +∠ BAC = 90° +∠BAC ∴∠ EAC =∠ BAG ∴△ AECABG≌△ (SAS) ∴∠ CEA =∠ ABG 你觉得什么样的四边形是正方形呢?