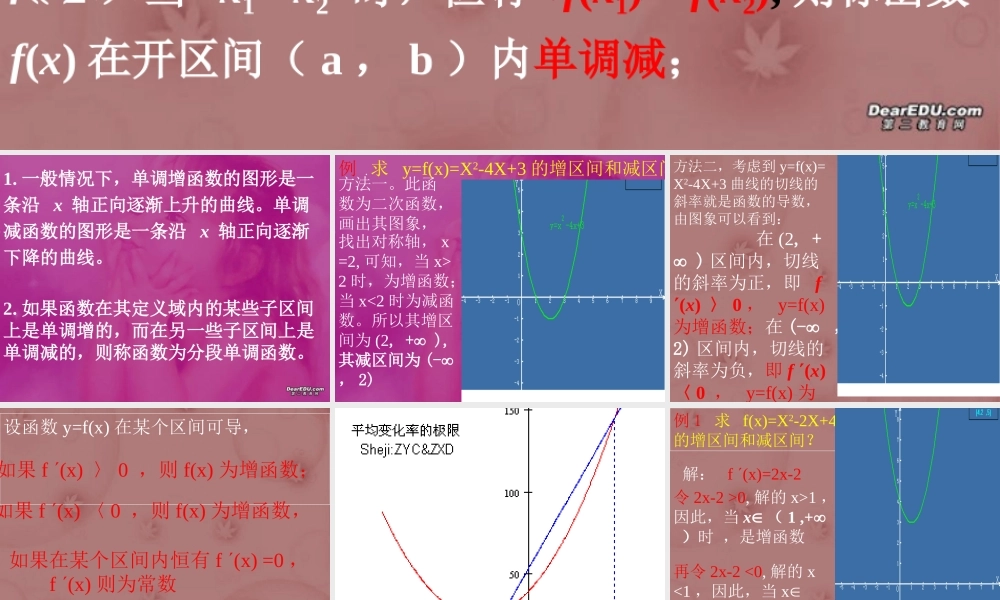
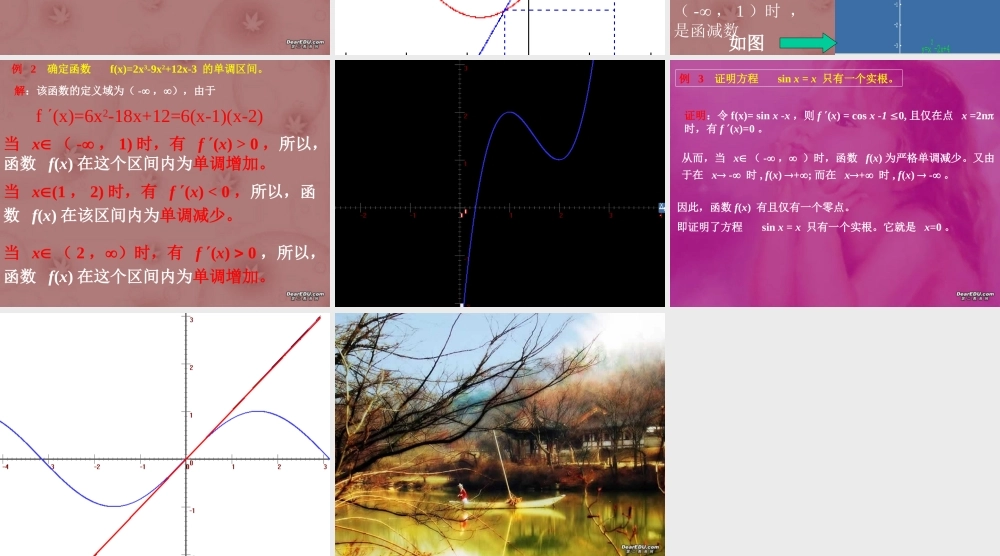
3.7 函数单调性的概念一,我们在函数的基本性质中曾经讨论过函数的单调性问题,在此我们再次回顾一下函数单调的定义。定义 设函数 f(x) 在区间( a , b )上有定义,如果对于区间( a , b )内的任意两点 x1 , x2 ,满足( 1 )当 x1 < x2 时,恒有 f(x1) < f(x2), 则称函数 f(x) 在开区间( a , b )内单调增; ( 2 )当 x1 < x2 时,恒有 f(x1) > f(x2), 则称函数 f(x) 在开区间( a , b )内单调减;1. 一般情况下,单调增函数的图形是一条沿 x 轴正向逐渐上升的曲线。单调减函数的图形是一条沿 x 轴正向逐渐下降的曲线。2. 如果函数在其定义域内的某些子区间上是单调增的,而在另一些子区间上是单调减的,则称函数为分段单调函数。例 .求 y=f(x)=X2-4X+3 的增区间和减区间?方法一。此函数为二次函数,画出其图象, 找出对称轴, x=2, 可知,当 x>2 时,为增函数;当 x<2 时为减函数。所以其增区间为 (2, + ),其减区间为 (- , 2)方法二,考虑到 y=f(x)=X2-4X+3 曲线的切线的斜率就是函数的导数,由图象可以看到: 在 (2, + ) 区间内,切线的斜率为正,即 f (x) 〉 0 , y=f(x)为增函数;在 (- ,2) 区间内,切线的斜率为负,即 f (x)〈 0 , y=f(x) 为增函数。设函数 y=f(x) 在某个区间可导, 如果 f (x) 〉 0 ,则 f(x) 为增函数;如果 f (x) 〈 0 ,则 f(x) 为增函数,如果在某个区间内恒有 f (x) =0 , f (x) 则为常数例 1 求 f(x)=X2-2X+4的增区间和减区间?解: f (x)=2x-2 令 2x-2 >0, 解的 x>1 ,因此,当 x ( 1 ,+ )时 ,是增函数再令 2x-2 <0, 解的 x<1 ,因此,当 x( - , 1 )时 ,是函减数如图例 2 确定函数 f(x)=2x3-9x2+12x-3 的单调区间。解:该函数的定义域为( - ,),由于f (x)=6x2-18x+12=6(x-1)(x-2)当 x ( - , 1) 时,有 f (x) > 0 ,所以,函数 f(x) 在这个区间内为单调增加。当 x(1 , 2) 时,有 f (x) < 0 ,所以,函数 f(x) 在该区间内为单调减少。当 x ( 2 ,)时,有 f (x) 0 ,所以,函数 f(x) 在这个区间内为单调增加。例 3 证明方程 sin x = x 只有一个实根。证明:令 f(x)= sin x -x ,则 f (x) = cos x -1 0, 且仅在点 x =2n时,有 f (x)=0 。从而,当 x ( - , )时,函数 f(x) 为严格单调减少。又由于在 x - 时 , f(x) +; 而在 x+ 时 , f(x) - 。因此,函数 f(x) 有且仅有一个零点。即证明了方程 sin x = x 只有一个实根。它就是 x=0 。