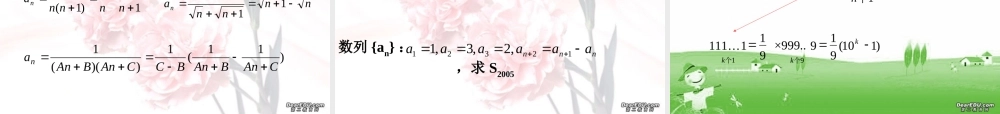数列复习 高三数学上学期期中考试复习课件集 人教版 高三数学上学期期中考试复习课件集 人教版VIP免费

高考数学总复习第 3 讲 数列一、基本知识归纳1 、一般数列[ 数列的通项公式 ] [ 数列的前 n 项和 ] )2()1(111nSSnSaannnnnaaaaS321…2 、等差数列[ 等差数列的概念 ][ 定义 ] 如果一个数列从第 2 项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母 d 表示。 [ 等差数列的判定方法 ]1 定义法：对于数列 {an} ，若 为常数 ，则数列是等差数列 2 等差中项：对于数列 {an} ，若 则数列是等差数列 daann1212nnnaaa [ 等差数列的通项公式 ]如果等差数列的首项是 a1 ，公差是 d ， 则等差数列的通项为 [ 说明 ] 该公式整理后 an 是关于 n 的一次函数。 dnaan)1(1 [ 等差数列的前 n 项和 ] 1 ． 2. [ 说明 ] 对于公式 2 整理后 an 是关于 n 的没有常数项的二次函数 2)( 1nnaanSdnnnaSn2)1(1 [ 等差中项 ]如果 a ， A ， b 成等差数列，那么 A 叫做 a 与 b的等差中项。即： 2A=a+b 或 [ 说明 ] ：在一个等差数列中，从第 2 项起，每一项（有穷等差数列的末项除外）都是它的前一项与后一项的等差中项；事实上等差数列中某一项是与其等距离的前后两项的等差中项 2baA[ 等差数列的性质 ]1 ．等差数列任意两项间的关系：如果 是等差数列的第 项， 是等差数列的第 项，且 ，公差为 ，则有 nanmamnm ddmnaamn)(  2. 对于等差数列 ，若 ， 则  naqpmnqpmnaaaa3 ．若数列 是等差数列， 是其前 n项的和， ，那么 ， ， 成等差数列  nanS*Nk kSkkSS2kkSS23 4 ．若等差数列 {an} 的前 2n-1 项的和为 ，等差数列 的前 2n-1 项的和为 ，则 12 nS nb'12 nS'1212nnnnSSba5 ．设数列 是等差数列， 是奇数项的和， 是偶数项的和， 是前 n 项的和，则有如下性质：  na奇S偶SnS1. 前 n 项的和偶奇SSSn2. 当 n 为偶数时， ，其中 d 为公差 d2nS奇偶S3. 当 n 为奇数时，则 ， ， ， ， （其中 是中间一项 )中偶奇aS S中奇a21nS中偶a21nS11SSnn偶奇中a3 、等比数列 [ 等比数列的概念 ][ 定义 ] 如果一个数列从第 2 项起，每一项与它的前一项的比等于同一个常数，那...