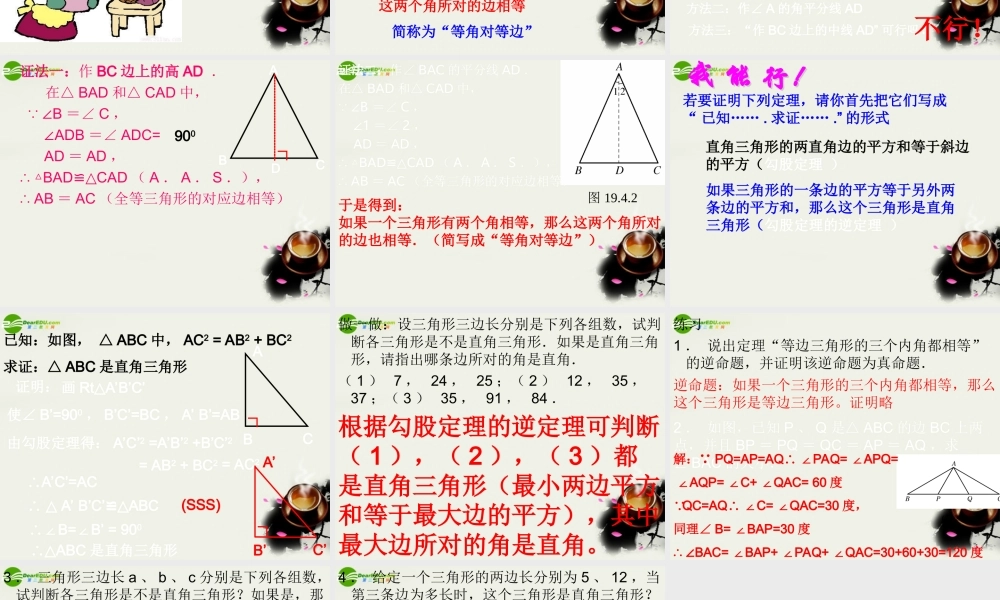
19.4.2 等腰三角形的判定等腰三角形定义是什么?有两条边相等的三角形等腰三角形性质定理等边对等角1 、在△ ABC 中, AC=BC, B=80∠0, 则∠ C=2 、等腰三角形的一个内角是 1000 ,则其余两个 角分别是3 、等腰三角形的一个内角是 700 ,则其余两个角 分别是 或4 、等腰三角形的两边长分别是 8cm 和 6cm , 则其周长是 cm5 、等腰三角形的两边长分别是 16cm 和 8cm , 则其周长是 cm200400 , 400550 , 550700 , 40022 或 20406 、下列命题中,正确的有( )( 1 )、有一个外角是 1200 的等腰三角形是等边三角形( 2 )有两个外角相等的等腰三角形是等边三角形( 3 )有一边上的高也是这边上的中线的等腰三角形是等边三角形( 4 )三个外角相等的三角形是等边三角形A 、 1 个 B 、 2 个 C 、 3 个 D 、 4 个B你有哪些方法可以判定一个三角形是等腰三角形?利用定义证明“ 中垂线性质”“ 等角对等边”一、等腰三角形性质定理:1 、将命题“等边对等角”写成“如果…那么…”的形式,并写出它的题设与结论。如果一个三角形有两条边相等,那么这两条边所对的角也相等2 、说出上述命题的逆命题,它是真命题还是假命题?如果一个三角形有两个角相等,那么这两个角所对的边相等简称为“等角对等边”二、“等角对等边”是真命题吗?已知:ABCD是,那么怎样来证明“等角对等边”方法:首先把命题写成“ 已知… .., 求证…… .” 的形式方法一:作 BC 边上的高 AD方法二:作∠ A 的角平分线 AD方法三:“作 BC 边上的中线 AD” 可行吗?在△ ABC 中,∠B=C∠,求证: AB=AC分析;要证 AB=AC ,可设法构造两个全等的三角形,使 AB , AC 分别是这两个三角形的对应边。∟不行!证法一:作 BC 边上的高 AD . 在△ BAD 和△ CAD 中, ∠B =∠ C , ∠ADB =∠ ADC= AD = AD , ∴ △BADCAD≌△( A . A . S .), ∴ AB = AC (全等三角形的对应边相等) 900ABC∟D证法二:作∠ BAC 的平分线 AD .在△ BAD 和△ CAD 中, ∠B =∠ C , ∠1 =∠ 2 , AD = AD ,∴ △BAD≌△CAD ( A . A . S .),∴ AB = AC (全等三角形的对应边相等) 图 19.4.2 于是得到:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)直角三角形的...