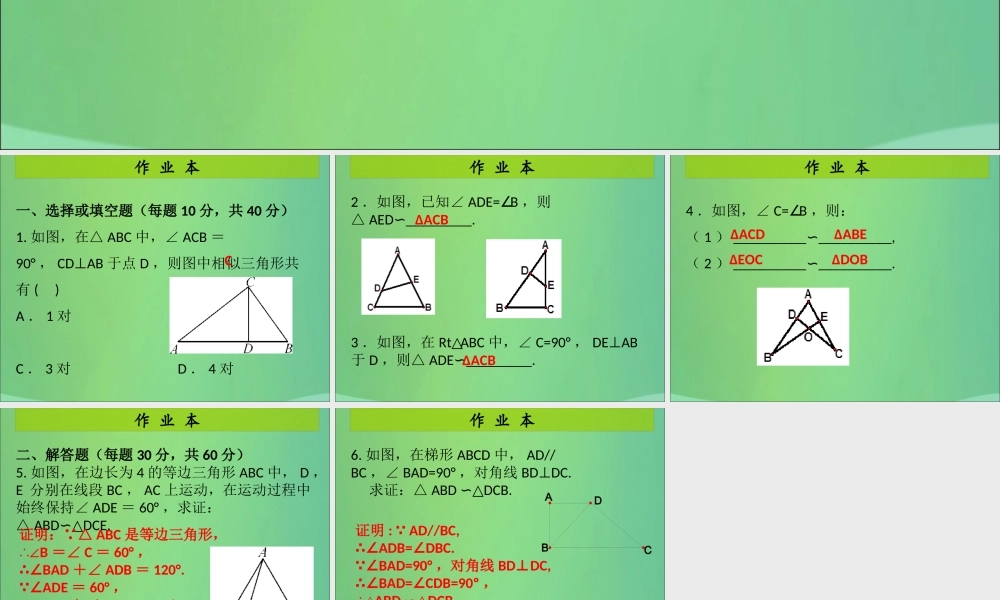
作 业 本第 5 课时 探索三角形相似的条件( 1 )第四章 图形的相似作 业 本一、选择或填空题(每题 10 分,共 40 分)1. 如图,在△ ABC 中,∠ ACB =90° , CDAB⊥于点 D ,则图中相似三角形共有 ( )A . 1 对 B . 2 对 C . 3 对 D . 4 对C作 业 本2 .如图,已知∠ ADE= B∠ ,则△ AED_________.∽3 .如图,在 Rt ABC△中,∠ C=90° , DEAB⊥于 D ,则△ ADE_________.∽ΔACBΔACB作 业 本4 .如图,∠ C= B∠ ,则:( 1 ) ____________________,∽( 2 ) ____________________.∽ΔACD ΔABE ΔEOC ΔDOB 作 业 本二、解答题(每题 30 分,共 60 分)5. 如图,在边长为 4 的等边三角形 ABC 中, D ,E 分别在线段 BC , AC 上运动,在运动过程中始终保持∠ ADE = 60° ,求证:△ ABDDCE.∽△ 证明:∵△ ABC 是等边三角形,∴∠B =∠ C = 60° ,∴∠BAD +∠ ADB = 120°.∵∠ADE = 60° ,∴∠ADB +∠ EDC = 120° ,∴∠DAB =∠ EDC ,∴△ABDDCE.∽△作 业 本6. 如图,在梯形 ABCD 中, AD//BC ,∠ BAD=90° ,对角线 BDDC.⊥ 求证:△ ABD DCB.∽△证明 : AD//BC, ∵∴∠ADB=DBC.∠∵∠BAD=90° ,对角线 BDDC,⊥∴∠BAD=CDB=90º∠,∴△ABD DCB.∽△ADBC