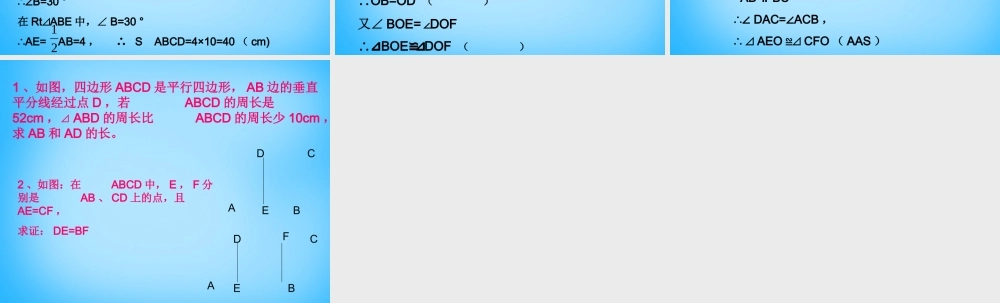
平行四边形性质训练选择题:1 、 ABCD 中,∠ A 比∠ B 大 20° 则∠ C 的度数为 ( )A 、 60 ° B 、 80 ° C 、 100° D 、 120°2 、ABCD 的周长为 40cm ,⊿ ABC 的周长为 25cm , 则对角 线 AC 长为()A 、 5cm B 、 15cm C 、 6cm D 、 16cm 3 、 ABCD 中, ∠ A=43 ° ,过点 A 作 BC 和 CD 的垂线,那么这两条垂线的夹角度数为 ( )A 、 113° B 、 115 ° C 、 137° D 、 90°CACM1﹑已知 : 如下图 ABCD 中 , 平行于对角线 AC的直线 MN 分别交 DA﹑ DC 的延长线于点 M﹑N, 交BA﹑BC 于点 PQ, 求证 :MQ=NPADBNQCP证明:∵四边形 ABCD 是平行四边形∴AD BC,AB CD∥∥即 AM CQ.∥又 AC MN,∥即 AC MQ∥∴ 四边形 MQCA 是平行四边形 ∴ MQ=AC同理可证:NP=AC∴ MQ=NP2 、已知 ABCD 中, AE⊥BD , AF⊥BD ,垂足为 E 、 F , 求证: EB=DFABCDEF证明:∵ AEBD⊥, CF BD⊥∴∠AEB=90° ,∠ CFD=90° ∴∠ AEB= CFD∠又四边形 ABCD 是平行四边形 ∴ AB=CD ,∠ ABE= CDF∠ ∴ ⊿ABECDF≌⊿ ∴ BE=DF ABCD中,∠ A=150° , AB=8cm , BC=10cm,求:四边形 ABCD 的面积ABCDE解:过点 A 作 AE ⊥ BC 交 BC 于 E 。∵ 四边形 ABCD 是平行四边形,∴AD BC∥∴∠BAD+ B=180∠° ∵ ∠BAD=150 °∴∠B=30 °在 Rt ABE⊿中,∠ B=30 °∴AE= AB=4 , ∴ S ABCD=4×10=40 ( cm)21已知如下图,在 ABCD 中, AC 与 BD 相交于点O ,点 E 、 F 在 AC 上,且 BE∥DF 。求证: BE=DFABCDOEF证明:∵ BE DF∥∴∠BEO= DFO∠( )∵ 四边形 ABCD 是平行四边形∴OB=OD ( )又∠ BOE= DOF∠∴⊿BOEDOF ≌⊿( )∴BE=DF ( )如图:在 ABCD 中, O 是对角线 AC和 BD 的交点, OE⊥AD 于 E , OF⊥BC于 F 。求证: OE=OFABCDEFO证明: ∵ OE⊥AD , OF⊥BC , ∴∠AEO= CFO=90 °∠ ∵ 四边形 ABCD 为平行四边形 ∴OA=OC ( ) AD BC∥ ∴∠ DAC= ACB∠, ∴ ⊿ AEO CFO≌⊿( AAS ) ∴ OE=OF1 、如图,四边形 ABCD 是平行四边形, AB 边的垂直平分线经过点 D ,若 ABCD 的周长是52cm ,⊿ ABD 的周长比 ABCD 的周长少 10cm ,求 AB 和 AD 的长。ABCDE2 、如图:在 ABCD 中, E , F 分别是 AB 、 CD 上的点,且AE=CF ,求证: DE=BFABCDEF