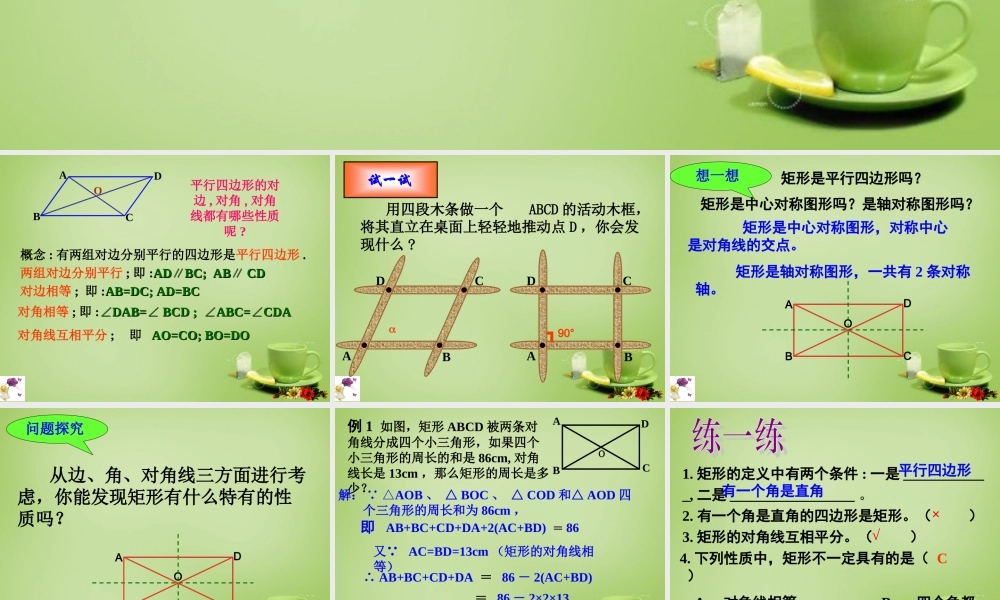
9.4 矩形的性质9.4 矩形的性质平行四边形的对边 , 对角 , 对角线都有哪些性质呢 ?概念 : 有两组对边分别平行的四边形是平行四边形 .OABDC 两组对边分别平行 ; 即 :ADBC; AB CD∥∥ADBC; AB CD∥∥对边相等 ; 即 :AB=DC; AD=BCAB=DC; AD=BC对角相等 ; 即 :DAB= BCD ; ABC=CDA∠∠∠∠DAB= BCD ; ABC=CDA∠∠∠∠对角线互相平分 ;即 AO=CO; BO=DOAO=CO; BO=DO 用四段木条做一个 ABCD 的活动木框,将其直立在桌面上轻轻地推动点 D ,你会发现什么 ?试一试DACB DACB ┓90°矩形是平行四边形吗?想一想 矩形是中心对称图形,对称中心是对角线的交点。 矩形是轴对称图形,一共有 2 条对称轴。矩形是中心对称图形吗?是轴对称图形吗?ABCDO问题探究 从边、角、对角线三方面进行考虑,你能发现矩形有什么特有的性质吗?ABCDO例 1 如图,矩形 ABCD 被两条对角线分成四个小三角形,如果四个小三角形的周长的和是 86cm, 对角线长是 13cm ,那么矩形的周长是多少? ∵ △AOB 、 △ BOC 、 △ COD 和△ AOD 四个三角形的周长和为 86cm ,又∵ AC=BD=13cm (矩形的对角线相等)∴ AB+BC+CD+DA = 86 - 2(AC+BD)= 86 - 2×2×13即矩形 ABCD 的周长等于 34cm 。解:OABDC = 34(cm)即 AB+BC+CD+DA+2(AC+BD) = 864. 下列性质中,矩形不一定具有的是( ) A 、对角线相等 B 、 四个角都相等 C 、对角线垂直 D 、是轴对称图形 1. 矩形的定义中有两个条件 : 一是 ____________, 二是 _________________ 。2. 有一个角是直角的四边形是矩形。( )3. 矩形的对角线互相平分。( ) 平行四边形有一个角是直角√×C5. 矩形具有而平行四边形不具有的性质是 ( ) A 两组对边分别平行 B 对角相等 C 对角线互相平分 D 对角线相等6. 矩形 ABCD 中,对角线 AC 、 BD 把矩形分成 ( ) 个等腰三角形。( A ) 2 ( B ) 4 ( C ) 6 ( D ) 8DBOABDC 例 2 如图,在矩形 ABCD 中, AB = 3 , BC = 4 , BEAC⊥于 E .试求出 AC 、BE 的长.解 : 在矩形 ABCD 中,∠ ABC = 90° ,AC = 22BCAB = 2243 = 25 = 5( 勾股定理 ) . 又∵ S△ ABC = AB·BC∴ BE =12= 2.4= AC·BE ,AB·BCAC=3×45ABDCE┒12小结:矩形:有一个角是直角的特殊平行四边形。矩形的性质:矩形的对角线相等且互相平分。 矩形具有平行四边形的所有性质;另外:矩形既是轴对称图形又是中心对称图形;矩形的四个内角都是直角。