数学 2.3.1平面向量数量积的物理背景与含义课件 新人教B版必修4 课件VIP免费

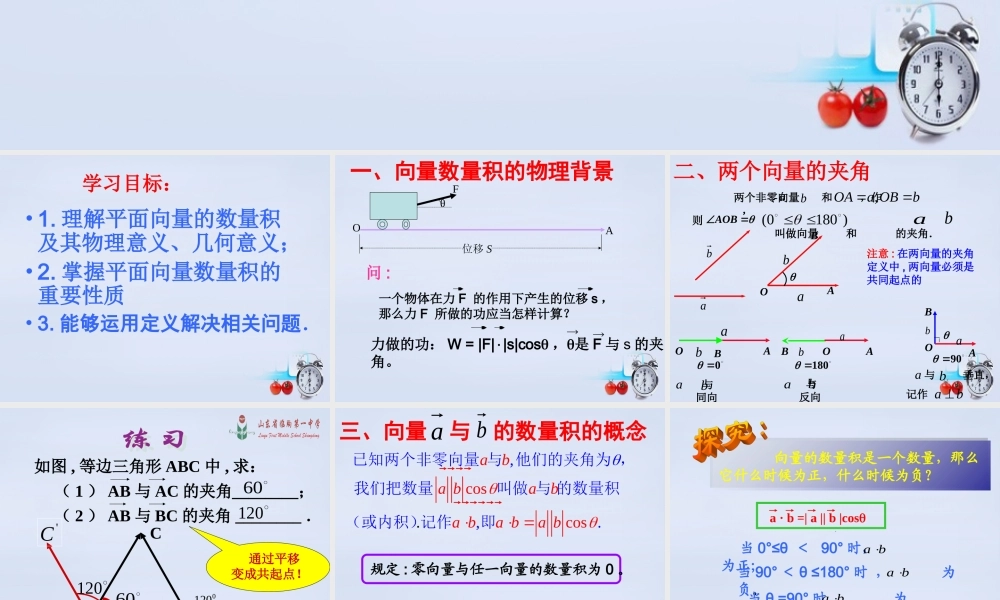
人教 B 版必修 42.3.1 平面向量数量积的物理背景及其含义学习目标：• 1. 理解平面向量的数量积及其物理意义、几何意义； • 2. 掌握平面向量数量积的重要性质• 3. 能够运用定义解决相关问题．位移 SOAFθ一、向量数量积的物理背景力做的功： W = |F||s|cos ，是 F 与 s 的夹角。问 :一个物体在力 F 的作用下产生的位移 s ，那么力 F 所做的功应当怎样计算？)1800( 两个非零向量 和 ，作 ，ab,OAa OBb�180 与 反向abOABabOAa0 与 同向abOABabaBbbAOBab则 叫做向量 和 的夹角．记作 ab90与 垂直，abOAB ab注意 : 在两向量的夹角定义中 , 两向量必须是共同起点的二、两个向量的夹角如图 , 等边三角形 ABC 中 , 求： （ 1 ） AB 与 AC 的夹角＿＿＿＿； （ 2 ） AB 与 BC 的夹角 ________ ．ABC 通过平移变成共起点！12060'CD012060120规定 : 零向量与任一向量的数量积为 0 。三、向量 与 的数量积的概念abcoscos,..,aba baba ba ba b 已知两个非零向量 与 他们的夹角为 ，我们把数量叫做 与 的数量积（或内积）记作即 向量的数量积是一个数量，那么它什么时候为正，什么时候为负？a · b =| a || b |cos当 90° ＜ θ ≤180° 时 ， 为负。 当 0°≤θ ＜ 90° 时， 为正； 当 θ =90° 时， 为零。a ba ba b注意注意： 数量积 a · b =| a || b |cos00a    注意公式变形，知三求一 .  “ · ” 不能省略不写，也不能写成“ ×” 一种新的运算abab不同，与、不同，它们表示数量；a ba b表示数量而不表示向量，与实数1.5,4,120.ababa b例 已知与 的夹角，求cosa ba b 解： 5 4 cos12015 4 ()102     OABbaa ba OBba１叫做向量 在向量 的方向上的投影的数量，即有向线段的数量1Bcosb数量积 a · b 等于 a 的模 | a | 与 b 在 a 的方向上的投影的数量 | b |cos  的乘积 .四、数量积的几何意义cosb数量积的几何意义投影的作图投影的作图 ::AOAOB| b |cos ...