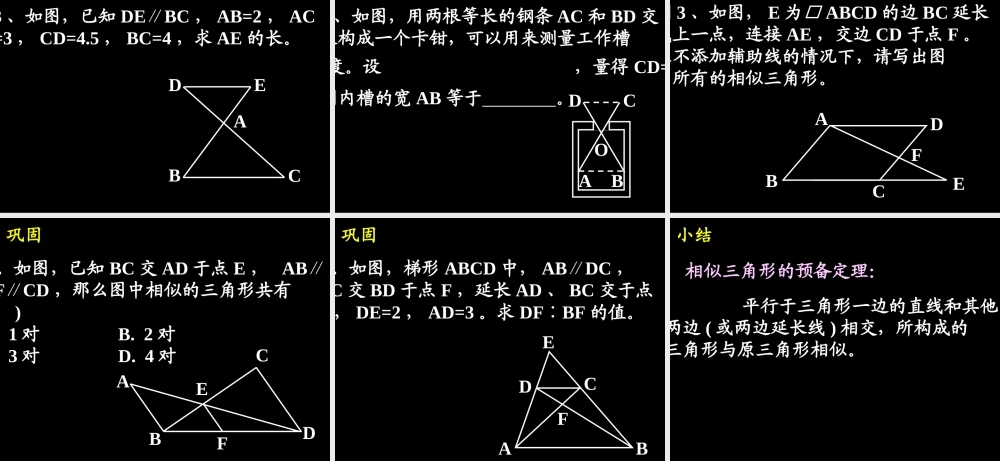
相似三角形的判定 (1) 相似三角形的判定 (1) 1 、怎样判定两个多边形相似?复习ABCDA’B’C’D’对应角相等,对应边的比相等 2 、怎样判定两个三角形相似?复习对应角相等,对应边的比相等FDECAB 一、如图,在△ ABC 中,点 D 是 AB 的中点, DEBC∥交 AC 于 E ,△ ABC 与△ADE 有什么关系?探究CABDEF 二、如图,在△ ABC 中,点 D 是 AB 上任意一点, DEBC∥交 AC 于 E ,那么△ABC 与△ ADE 有什么关系?探究CABDE 归纳相似三角形的预备定理: 平行于三角形一边的直线和其他两边 ( 或两边延长线 ) 相交,所构成的三角形与原三角形相似。 范例例 1 、如图,△ ABC 中, DEBC∥, AB=8cm , AC=6cm , AE=4cm , DE=5cm,求 AD 、 BC 的长。CABDE 巩固2 、如图,△ ABC 中, DEBC∥, AD=6cm , BD=2cm , AE=4cm ,求 EC 的长。CABDE 三、如图,在△ ABC 中,点 D 是 AB 延长线上一点, DEBC∥交 AC 的延长心于 E ,△ ABC 与△ ADE 有什么关系?探究EADBC 归纳相似三角形的预备定理: 平行于三角形一边的直线和其他两边 ( 或两边延长线 ) 相交,所构成的三角形与原三角形相似。( 或两边延长线 ) 四、如图,在△ ABC 中,点 D 是 AB 反向延长线上一点, DEBC∥交 AC 的反向延长线于 E ,△ ABC 与△ ADE 有什么关系?探究EADBC 归纳相似三角形的预备定理: 平行于三角形一边的直线和其他两边 ( 或两边延长线 ) 相交,所构成的三角形与原三角形相似。( 或两边延长线 ) 范例例 2 、如图,已知 DEBC∥, AB=2 , AC=3 , AD=1.5 , BC=4 ,求 AE 、 DE 的长。EADBC 巩固3 、如图,已知 DEBC∥, AB=2 , AC=3 , CD=4.5 , BC=4 ,求 AE 的长。EADBC 巩固4 、如图,用两根等长的钢条 AC 和 BD 交叉构成一个卡钳,可以用来测量工作槽的宽度。设 ,量得 CD=n ,mODOBOCOA则内槽的宽 AB 等于 。ACBDO 范例例 3 、如图, E 为□ ABCD 的边 BC 延长线上一点,连接 AE ,交边 CD 于点 F 。在不添加辅助线的情况下,请写出图中所有的相似三角形。DABCEF 巩固5 、如图,已知 BC 交 AD 于点 E , AB∥EFCD∥,那么图中相似的三角形共有( )A. 1 对 B. 2 对C. 3 对 D. 4 对CBAEFD 巩固6 、如图,梯形 ABCD 中, ABDC∥,AC 交 BD 于点 F ,延长 AD 、 BC 交于点E , DE=2 , AD=3 。求 DFBF∶的值。DABCFE 小结相似三角形的预备定理: 平行于三角形一边的直线和其他两边 ( 或两边延长线 ) 相交,所构成的三角形与原三角形相似。