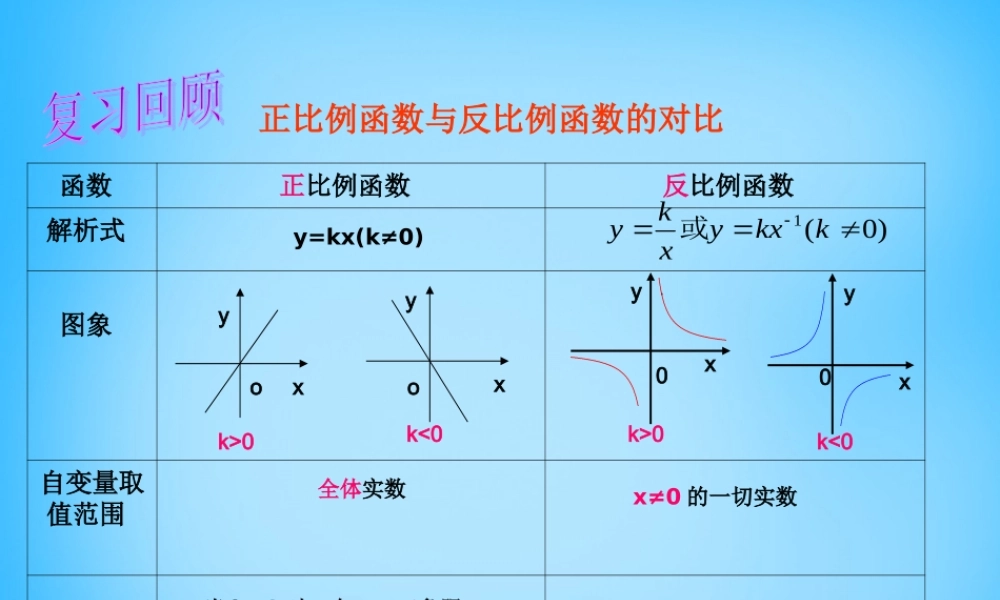
函数 正比例函数 反比例函数 解析式 图象 自变量取值范围 图象的位置 性质 当 k>0 时, y 随 x 的增大而减小 当 k<0 时, y 随 x 的增大而增大正比例函数与反比例函数的对比y=kx(k≠0) 全体实数 x≠0 的一切实数 当 k>0 时,在一、三象限; 当 k<0 时,在二、四象限。 当 k>0 时,在一、三象限;当 k<0 时,在二、四象限当 k>0 时, y 随 x 的增大而增大当 k<0 时, y 随 x 的增大而减小k<0xyoxyok>0k<0yx0y0k>0x)0(1kkxyxky或D先假设某个函数图象已经画好,再确定另外的是否符合条件 .1 、如图,函数 和 y= - kx+1(k≠0) 在同一坐标系内的图象大致是 ( )kyx642-2-4-55Oyx642-2-4-55Oyx642-2-4-55Oyx642-2-4-55Oyxyy33< y< y11< y< y222 、函数 的图象上有三点(- 3,y1 ) , (- 1,y2 ) , ( 2,y3 ) , 则函数值 y1 、 y2 、 y3的 大小关系是 _______________;为常数)kxky(22 3. 已知 y 与 x 成反比例 , 并且当 x = 2 时 y = 5 ,求 x 与 y 的函数关系式。 x10y = 4. 根据图形写出函数的解析式。 xy0( -3 ,1 )y = x35. 点 A 是反比例函数图象上一点,自 A 作 y 轴垂线段,垂足为 T ,已知 S AOT△=4 ,则函数表达式为 ( )xyoATABCD4yx8yx16yx8yxD例题讲解例 1. 如图,已知点 A(4, m) , B(-1, n) 在反8yx与 x 轴交于点 C ,如果点 D 在 y 轴上,且 DA=DC ,求点 D 的坐标。比例函数 的图象上,直线 ABxyoDACB试一试1. 如图,点 P 在经过点 B(0, -2) , C(4, 0)3yx的图象上,若 PQ∥y轴,求点 Q 的坐标。的直线上,且纵坐标为 -1 ,点 Q 在xyoBC-1PQ例题 讲解例 2. 如图,一次函数和反比例函数的图象分别是直线AB 和双曲线,直线 AB 与双曲线的一个交点为 C ,CD⊥x 轴于点 D ,已知 OD=2OB=4OA=4 ,求一次函数和反比例函数的解析式。xyoCABD练一练1. 如图,点 A 在第一象限,它的纵坐标12yxxyoCAB图象经过点 A 。是横坐标的 3 倍,反比例函数 的(1) 求点 A 的坐标;(2) 如果经过点 A 的直线与如果经过点 A的直线与 y 轴的正半轴交于点 B ,且 OB=AB ,求直线方程。xyoCAB2. 如图,一次函数 的图象与yaxb反比例函数 的图象交于点 A(1,4) , B(3,m) 两点。kyx(1) 求一次函数的解析式;xyoA(1,4)B(3,m)(2) 求△ AOB 的面积。课堂小结一次函数与反比例函数的综合运用再 见