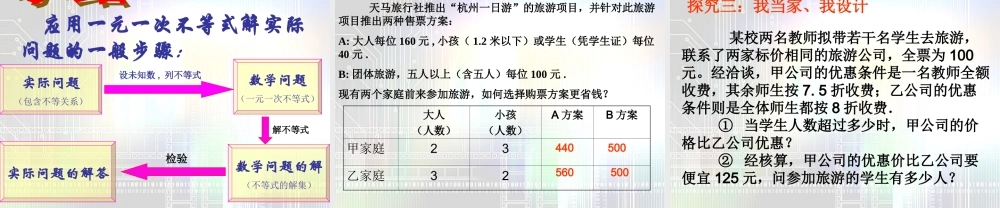
9.2.1 实际问题 与一元一次不等式 解下列不等式,并在数轴上表示解集:)5(3)5(2 )2(14)3(5 )1(xxxx 解:移项得:5x-4x>-1-15合并得X>-16解集在数轴上的表示如图0-16( 1 ) 5(x+3)>4x-1去括号得:3x+15>4x-1 解:移项得:2x-3x < -10-15合并得 : -X < -25解集在数轴上的表示如图( 2 ) 2(x+5) < 3 ( x-5 )去括号得:2x+10 < 3x-15x > 252505系数化为 1 得: 某学校计划购实若干台电脑,现从两家商店了解到同一型号的电脑每台报价均为 6000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原报价收款,其余每台优惠 25 %;乙商场的优惠条件是:每台优惠20 %.如果你是校长,你该怎么考虑,如何选择?知识探究 1: 思考? (1) 什么情况下,到甲商场购买更优惠? (2) 什么情况下,到乙商场购买更优惠? (3) 什么情况下,两个商场收费相同?如果设购买 x 台电脑 : 解:设购买 x 台电脑,(1) 如果到甲商场购买更优惠,则 6000 + 6000 ( 1 - 25 %)( x - 1 )< 6000 ( 1 - 20%) x去括号,得: 6000 + 4500x - 4500 < 4800x移项且合并,得:- 300x < -1500不等式两边同除以- 300 ,得: x5﹥答:购买 5 台以上电脑时,甲商场更优惠. (2) 、( 3 )略 我店累计购买 100 元商品后,再购买的商品按原价的 90% 收费甲我店累计购买 50 元商品后,再购买的商品按原价的 95% 收费乙探究 2 甲乙 如果你要分别购买 40 元、80 元、 140 元、160 元商品,应该去哪家商店更优惠?甲商店购物款达多少元后可以优惠?乙商店购物款达多少元后可以优惠?10050 甲店:100+40×90%=136 (元)乙店:50+90×95%=135.5 (元)甲店乙店>甲店:100+60×90%=154( 元)50+110×95%=154.5(元)乙店:甲店<乙店 当购买 140 元商品时:当购买 160 元商品时: 分析:乙店消费>甲店消费解:设累计购物 x 元( x > 100 ),如果在甲店购物花费小,则50+0.95 ( x-50 )100+0.9 ( x-100 )>去括号得: 50+0.95x-47.5>100+0.9x-90移项且合并得: 0.05x>7.5系数化为 1 得:X >150∴ 累计购物超过 150 元时在甲店购物花费小。 如果累计购物超过 100 元,那么在甲店购物花费小吗?思考: 2 累计购物多少元时在乙店购物花费与在甲店一样? 3 累计购物多少元时在乙店购物花费更小? ...