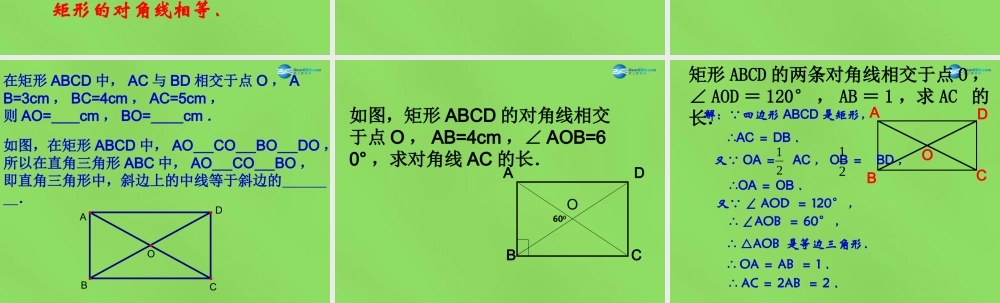
《 19 . 3 . 1 矩形》做一做如图, BO 是 Rt△ABC 斜边 AC 上的中线,请画出△ ABC 关于点 O 对称的图形.D四边形 ABCD 有什么特点?ABCO四边形 ABCD 有什么特点?有一个角是直角的平行四边形叫做矩形( 长方形 ) .矩形是一个特殊的平行四边形.ACBD如图是一个平行四边形的活动框架,对角线是两根橡皮筋,改变框架的形状 :⑴ 当框架改变到 ( 符合某一条件时 ) ,该四边形就为矩形.⑵ 当框架变化到矩形时,请比较两条对角线的大小.说明你的理由.如图是一个平行四边形的活动框架,对角线是两根橡皮筋,改变框架的形状 :矩形的对角线相等.请你总结矩形的有关性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:推论:直角三角形斜边上的中线等于斜边的一半. 如图,矩形 ABCD 中,对角线 AC 、 BD 相交于点 O ,请探讨 OC 与 BD 的关系OADCB在矩形 ABCD 中, AC 与 BD 相交于点 O , AB=3cm , BC=4cm , AC=5cm ,则 AO= cm , BO= cm . 如图,在矩形 ABCD 中, AO CO BO DO ,所以在直角三角形 ABC 中, AO CO BO ,即直角三角形中,斜边上的中线等于斜边的 . OADCBABCDO如图,矩形 ABCD 的对角线相交于点 O , AB=4cm ,∠ AOB=60° ,求对角线 AC 的长.600矩形 ABCD 的两条对角线相交于点 O ,∠ AOD = 120° , AB = 1 ,求 AC 的长.ABCDO解:∵四边形 ABCD 是矩形,∴AC = DB .又∵ OA = AC , OB = BD , 2121∴OA = OB .又∵ ∠ AOD = 120° , ∴ ∠AOB = 60° , ∴ △AOB 是等边三角形. ∴ OA = AB = 1 . ∴ AC = 2AB = 2 .