九年级数学下册 281 锐角三角函数(第2课时)课件2 (新版)新人教版 课件VIP免费

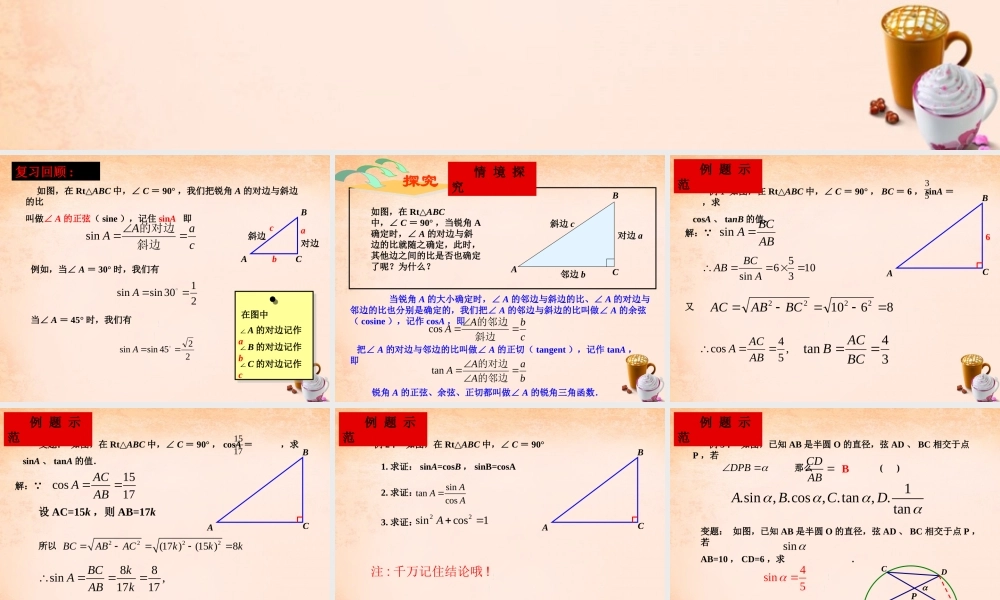
如图，在 Rt△ABC 中，∠ C ＝ 90° ，我们把锐角 A 的对边与斜边的比叫做∠ A 的正弦（ sine ），记住 sinA 即caAA斜边的对边sin例如，当∠ A ＝ 30° 时，我们有2130sinsinA当∠ A ＝ 45° 时，我们有2245sinsinAABCcab对边斜边在图中∠A 的对边记作a∠B 的对边记作b∠C 的对边记作c复习回顾 :探究如图，在 Rt△ABC中，∠ C ＝ 90° ，当锐角 A确定时，∠ A 的对边与斜边的比就随之确定，此时，其他边之间的比是否也确定了呢？为什么？ABC邻边 b对边 a斜边 c 当锐角 A 的大小确定时，∠ A 的邻边与斜边的比、∠ A 的对边与邻边的比也分别是确定的，我们把∠ A 的邻边与斜边的比叫做∠ A 的余弦（ cosine ），记作 cosA ，即cbAA斜边的邻边cos 把∠ A 的对边与邻边的比叫做∠ A 的正切（ tangent ），记作 tanA ，即baAAA的邻边的对边tan 锐角 A 的正弦、余弦、正切都叫做∠ A 的锐角三角函数． 情 境 探 究 例 1 如图，在 Rt△ABC 中，∠ C ＝ 90° ， BC ＝ 6 ， sinA ＝ ，求cosA 、 tanB 的值．53解： ABBCA sin10356sinABCAB又86102222BCABAC,54cosABACA34tanBCACBABC6 例 题 示 范 变题： 如图，在 Rt△ABC 中，∠ C ＝ 90° ， cosA ＝ ，求sinA 、 tanA 的值．1517解： 15cos17ACAAB88sin,1717BCkAABk88tan1515BCkAACkABC 例 题 示 范设 AC=15k ，则 AB=17k所以2222(17 )(15 )8BCABACkkk 例 2 ： 如图，在 Rt△ABC 中，∠ C ＝ 90° 例 题 示 范1. 求证： sinA=cosB ， sinB=cosA2. 求证：sintancosAAA3. 求证：22sincos1AABC注 : 千万记住结论哦 ! 例 3 ： 如图，已知 AB 是半圆 O 的直径，弦 AD 、 BC 相交于点P ，若 例 题 示 范DPB 那么 ( )CDAB 1.sin, .cos , .tan,. tanABCDB变题： 如图，已知 AB 是半圆 O 的直径，弦 AD 、 BC 相交于点 P ，若AB=10 ， CD=6 ，求 .sinOCDBAP4sin5 1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值．练习：解：由勾股定理222213125BCABACABC13125sin13BCAAB12cos13ACAAB5tan12BCAAC12sin13ACBAB5cos13BCBAB12tan5ACBBC...