新疆哈密市高二数学(141 正弦函数、余弦函数的图像)课件 新人教版必修3 课件VIP免费

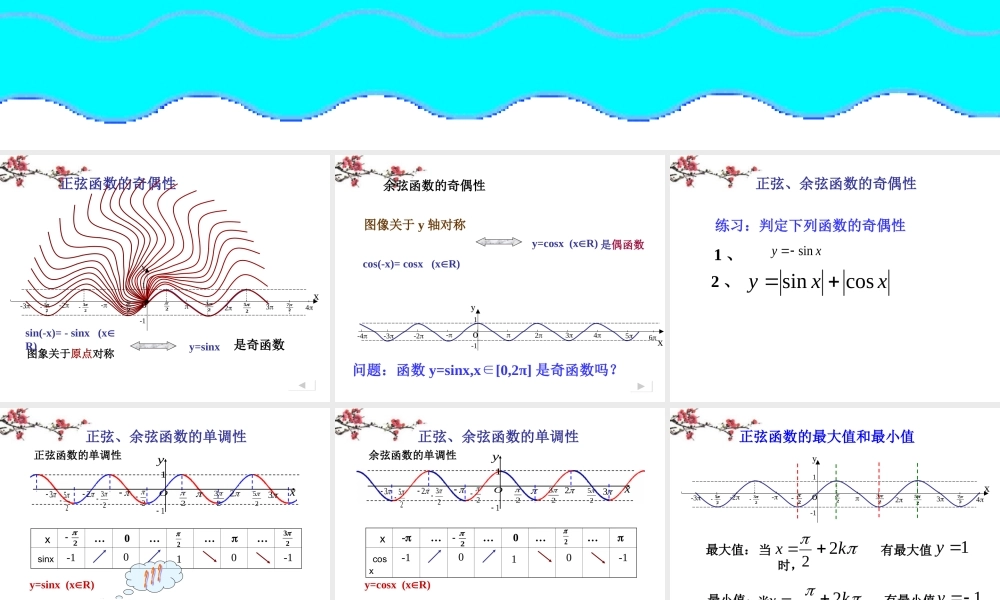
正弦、余弦函数的性质（奇偶性、单调性、最值）斗奋拼搏 正弦函数的奇偶性 y=sinxyxo--1234-2-31223252722325 图象关于原点对称是奇函数sin(-x)= - sinx (xR) x6o--12345-2-3-41ycos(-x)= cosx (xR) y=cosx (xR) 是偶函数 余弦函数的奇偶性图像关于 y 轴对称问题：函数 y=sinx,x[0,2π]∈是奇函数吗？ 练习：判定下列函数的奇偶性 正弦、余弦函数的奇偶性xysinxxycossin 1 、2 、 正弦、余弦函数的单调性 正弦函数的单调性 y=sinx (xR)增区间为 [ ， ] 其值从 -1 增至122 x sinx2223 … 0 … …  …-1 0 1 0 -1减区间为 [ ， ] 其值从 1 减至 -1223[ +2k, +2k],kZ22[ +2k, +2k],kZ223x22322523yO23225311 正弦、余弦函数的单调性 余弦函数的单调性 y=cosx (xR) x cosx22 - … … 0 … … -1 0 1 0 -1增区间为 其值从 -1 增至 1[ +2k, 2k],kZ减区间为 ， 其值从 1 减至 -1[2k, 2k + ], kZx22322523yO23225311 正弦函数的最大值和最小值 xyo--1234-2-31223252722325最大值：有最大值1yk2最小值：2x当 时，有最小值1yk22x当 时， 余弦函数的最大值和最小值最大值：0x当 时，有最大值1yk2最小值：x当 时，有最小值1yk2yxo--1234-2-31223252722325 例 1. 下列函数有最大、最小值吗？如果有，请写出取最大、最小值时的自变量 x 的集合，并说出最大、最小值分别是什么 .cos1,3sin 2 ,.yxxRyx xR(1);(2)解：这两个函数都有最大值、最小值 .（ 1 ）使函数 取得最大值的 x 的集合，就是使函数 取得最大值的 x 的集合cos1,yxxRcos ,yx xR{ |2,}x xkkZ 使函数 取得最小值的 x 的集合，就是使函数 取得最小值的 x 的集合cos1,yxxRcos ,yx xR{ |(21) ,}x xkkZ 函数 的最大值是 1+1=2 ；最小值是-1+1=0.cos1,yxxR 解：（ 2 ）令 t=2x, 因为使函数 取最大值的 t 的集合是3sin ,yt tR{ |2,}2t tk...