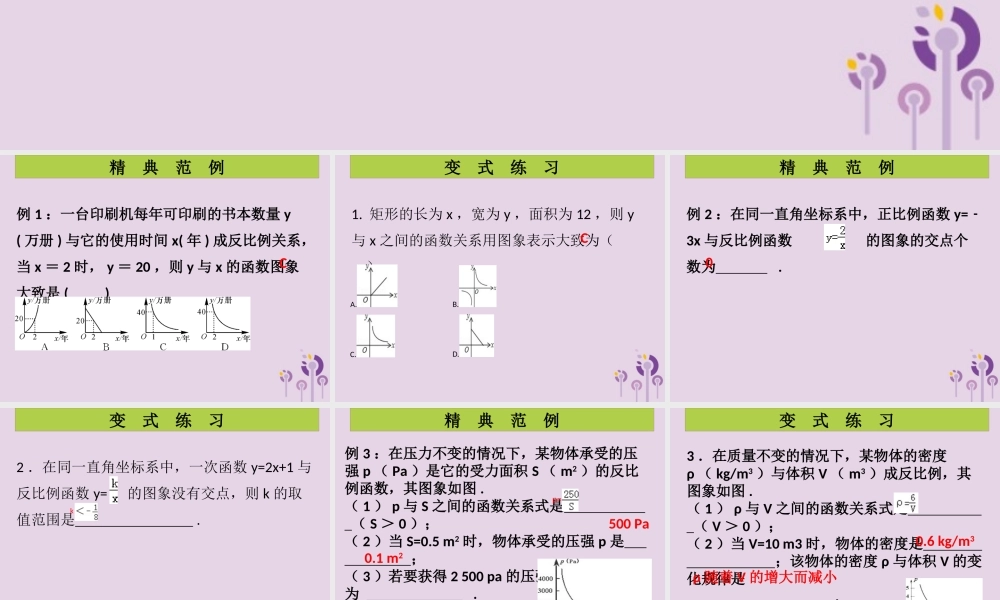
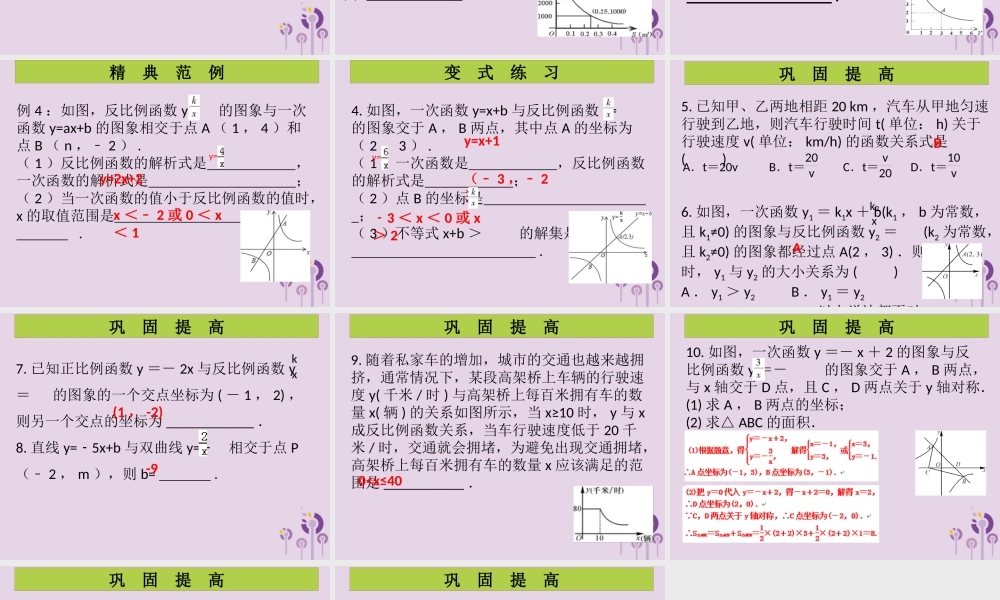
巩固提高精典范例(变式练习)第 4 课时 反比例函数的应用第六章 反比例函数例 1 :一台印刷机每年可印刷的书本数量 y( 万册 ) 与它的使用时间 x( 年 ) 成反比例关系,当 x = 2 时, y = 20 ,则 y 与 x 的函数图象大致是 ( )精 典 范 例C1. 矩形的长为 x ,宽为 y ,面积为 12 ,则 y与 x 之间的函数关系用图象表示大致为( )变 式 练 习CA. B. C. D. 例 2 :在同一直角坐标系中,正比例函数 y=﹣3x 与反比例函数 的图象的交点个数为 .精 典 范 例02 .在同一直角坐标系中,一次函数 y=2x+1 与反比例函数 y= 的图象没有交点,则 k 的取值范围是 .变 式 练 习k 例 3 :在压力不变的情况下,某物体承受的压强 p ( Pa )是它的受力面积 S ( m2 )的反比例函数,其图象如图 .( 1 ) p 与 S 之间的函数关系式是 ( S > 0 );( 2 )当 S=0.5 m2 时,物体承受的压强 p 是 ;( 3 )若要获得 2 500 pa 的压强,受力面积应为 .精 典 范 例500 Pa0.1 m2p= 变 式 练 习3 .在质量不变的情况下,某物体的密度ρ ( kg/m3 )与体积 V ( m3 )成反比例,其图象如图 .( 1 ) ρ 与 V 之间的函数关系式是 ( V > 0 );( 2 )当 V=10 m3 时,物体的密度是 ;该物体的密度 ρ 与体积 V 的变化规律是 .0.6 kg/m3ρ 随着 V 的增大而减小例 4 :如图,反比例函数 y= 的图象与一次函数 y=ax+b 的图象相交于点 A ( 1 , 4 )和点 B ( n ,﹣ 2 ) .( 1 )反比例函数的解析式是 ,一次函数的解析式是 ;( 2 )当一次函数的值小于反比例函数的值时,x 的取值范围是 .精 典 范 例y=2x+2x <﹣ 2 或 0 < x< 1y= 4. 如图,一次函数 y=x+b 与反比例函数 y= 的图象交于 A , B 两点,其中点 A 的坐标为( 2 , 3 ) .( 1 )一次函数是 ,反比例函数的解析式是 ;( 2 )点 B 的坐标是 ;( 3 )不等式 x+b > 的解集是 .变 式 练 习y=x+1(﹣ 3 ,﹣ 2)﹣3 < x < 0 或 x> 2y= 巩 固 提 高5. 已知甲、乙两地相距 20 km ,汽车从甲地匀速行驶到乙地,则汽车行驶时间 t( 单位: h) 关于行驶速度 v( 单位: km/h) 的函数关系式是( )6. 如图,一次函数 y1 = k1x + b(k1 , b 为...