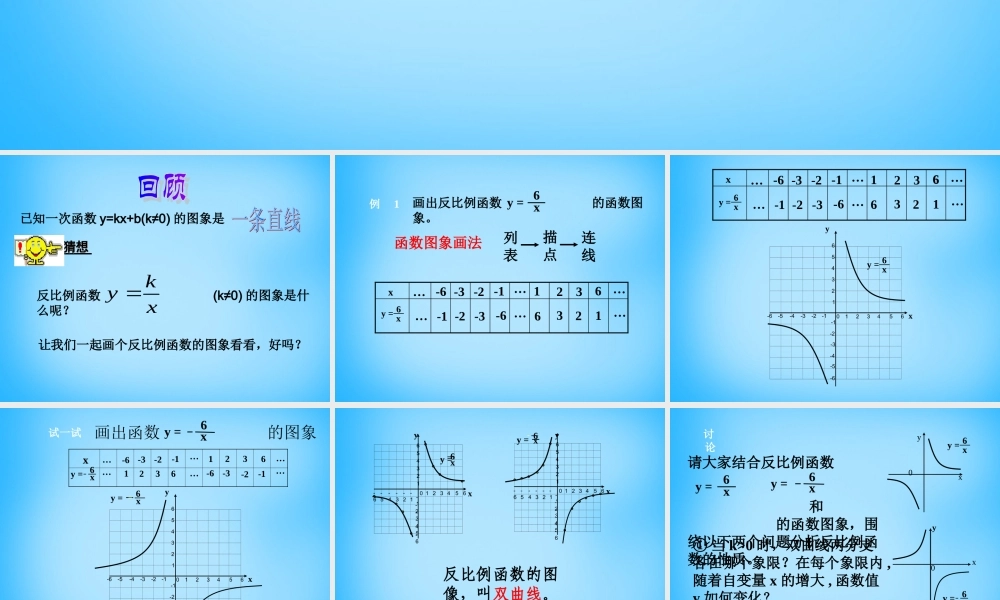
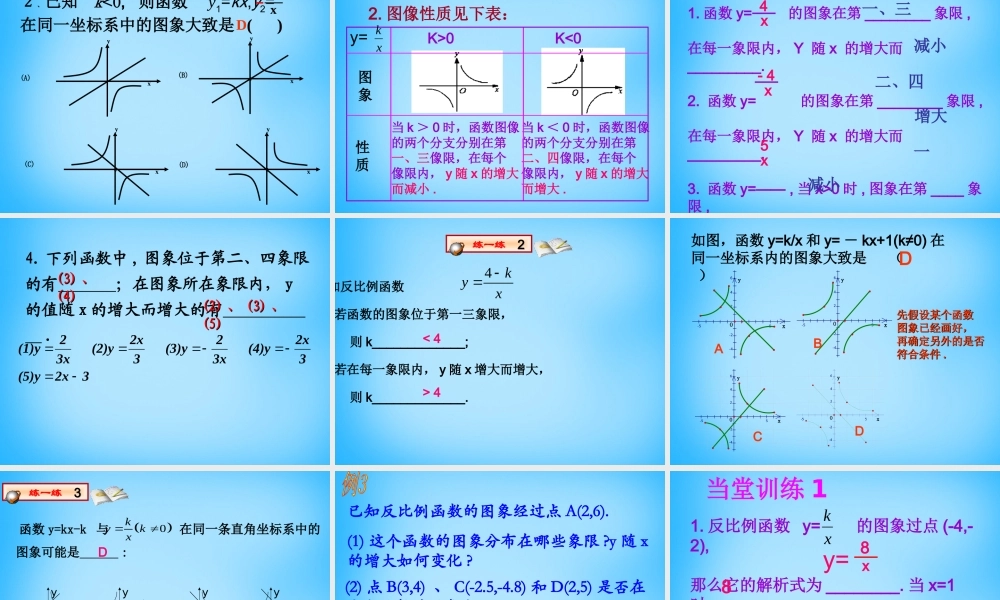
反比例函数的图象与性质已知一次函数 y=kx+b(k≠0) 的图象是反比例函数 (k≠0) 的图象是什么呢?xky 让我们一起画个反比例函数的图象看看,好吗?猜想猜想猜想猜想画出反比例函数 的函数图象。 y = x6 函数图象画法列表描点连线例 1 xy = x616233261-1-6-2-3-3-2-6-1………………y = x6 xy = x6162332616-1-6-2-3-3-2-6-1………………123456-1-3-2-4-5-61234-1-2-3-40-6-556xyy = - x6 xy = x6-6…1…画出函数 的图象y = x6试一试1236-1-2-3…-663-32-2-1………123456-1-3-2-4-5-61234-1-2-3-40-6-556xyy1 2 3 456-1-3-2-4-5-61234-1-2-3-40-6-556xy =x61 2 3 45 6-1-3-2-4-5-61234-1-2-3-40-6-556yxy = - x6反比例函数的图像,叫双曲线。 讨 论① 当 k>0 时,双曲线两分支各在哪个象限?在每个象限内 ,随着自变量 x 的增大 , 函数值y 如何变化?请大家结合反比例函数 和 的函数图象,围绕以下两个问题分析反比例函数的性质。 y =x6y = x6xy0xy0② 当 k<0 呢 ?y = x6y = x6x456 函数图象的两个分支分别在第一、三象限内。2 、在每个象限内,曲线从左向右下降,也就是在每个象限内 y 随 x 的增大而减小。3 、图象的两个分支都无限接近于 x 轴和 y 轴,但不会与 x 轴和 y 轴相交。y0123123456y= 6x1 、当 k > 0 时,探 究 函数图象的两个分支分别在第二、四象限内。2 、在每个象限内,曲线从左向右上升,也就是说在每个想象内, y 随 x 的增大而增大。3 、图象的两个分支都无限接近与 x 轴和 y 轴,但不会和 x 轴和 y 轴相交。-40-51-3yx2345-16-2-61y=6x1 、当 k < 0 时,探 究函数 的图象在第 ________ 象限 ,在每一象限内, y 随 x 的增大而 _________. 函数 的图象在第 ________ 象限 ,在每一象限内, y 随 x 的增大而 _________.函数 , 当 x>0 时 , 图象在第 ____象限 ,y 随 x 的增大而 _________.一、三二、四一减小增大减小yx30yx20yx练一练11练 习4 、在同一坐标系中 , 函数 y=-kx+k ( k≠0 )与 的大致图象应是 ( )y = xkABDCCA :xyoB:xyoD:xyoC :xyo1 、反比例函数 y= - 的图象大致是( ) x5D2 . 若关于 x,y 的函数 图象位于第一、三象限, 则 k 的取值范围是 _______________xky1+k>k> -- 113 . 甲乙两地相距 100km ...