人教版高一数学已知三角函数值求角 课件VIP免费

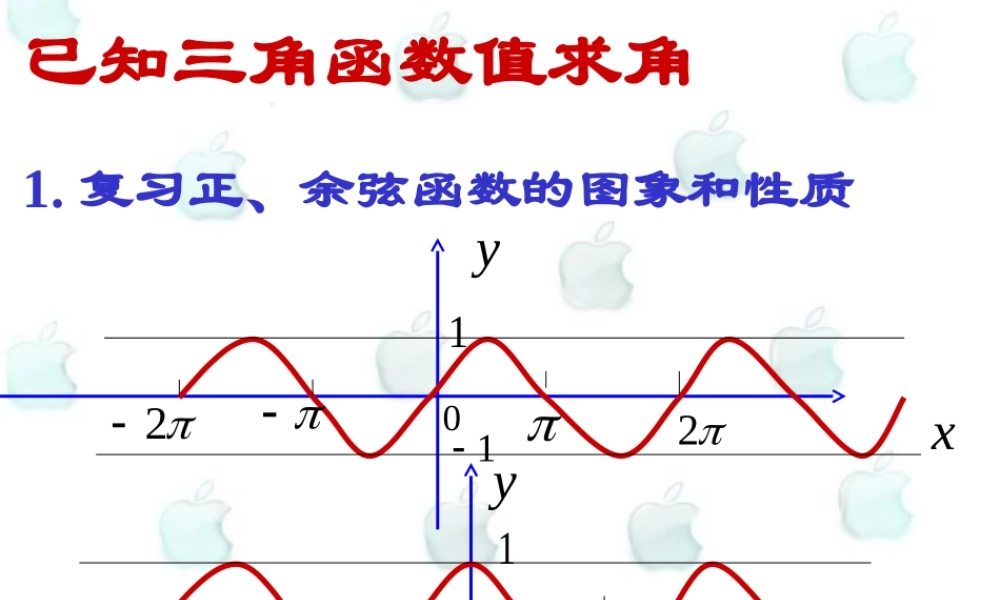
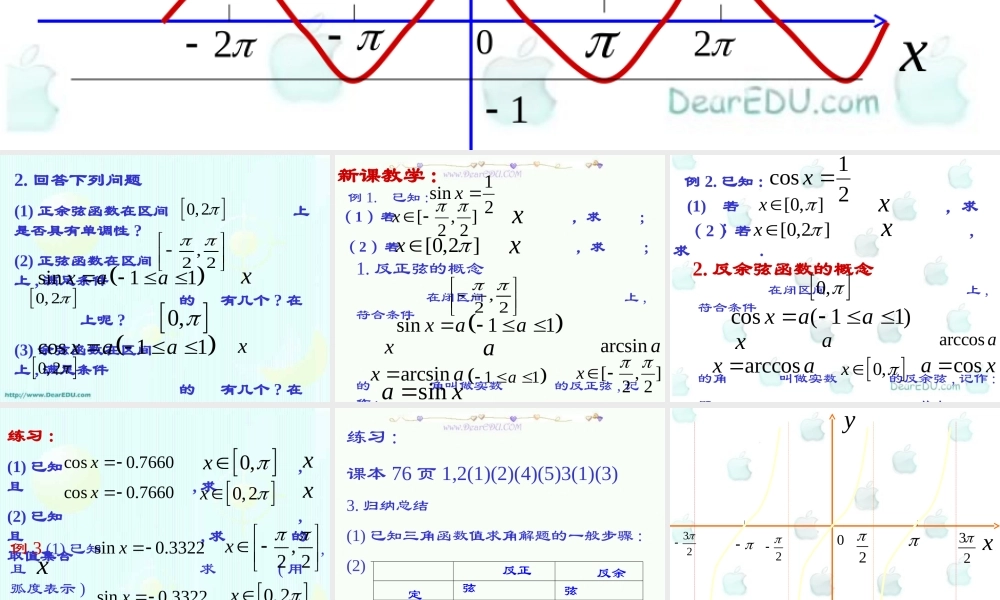
已知三角函数值求角 1. 复习正、余弦函数的图象和性质00yyxx222211112. 回答下列问题(1) 正余弦函数在区间 上是否具有单调性 ?(2) 正弦函数在区间 上 , 满足条件 的 有几个 ? 在 上呢 ?(3) 余弦函数在区间 上 , 满足条件 的 有几个 ? 在 上呢 ?0,20,20,2,22 0,sin11xaa cos11xaa xx新课教学 : 例 1. 已知 :21sinx（ 1 ）若 ，求 ；]2,2[xx （ 2 ）若 ，求 ；]2,0[xx1. 反正弦的概念 在闭区间 上 ,符合条件 的 角叫做实数 的反正弦 , 记作 :即 其中 且,22 sin11xaa xaarcsin aarcsinxa11a ]2,2[xsinax例 2. 已知 :21cosx[0, ]x(1) 若 ，求 ；x （ 2 ）若 , 求 .]2,0[xx2. 反余弦函数的概念 在闭区间 上 ,符合条件 的角 叫做实数 的反余弦 , 记作 :即 其中 且0,cos( 11)xaa xaarccosaarccosxa0,xcosax练习 :(1) 已知 ,且 , 求(2) 已知 ,且 , 求 的取值集合cos0.7660x 0,xxcos0.7660x 0,2xx例 3.(1) 已知 ,且 求 ( 用弧度表示 ) (2) 已知 , 且 求 的取值集合sin0.3322x ,2 2x  x0,2xxsin0.3322x 练习 :课本 76 页 1,2(1)(2)(4)(5)3(1)(3)3. 归纳总结(1) 已知三角函数值求角解题的一般步骤 :(2) 定 义 记 法 取值范围 反正弦 反余弦yx2232320例 4. 已知 :31tanx（ 1 ）若 ，求 （精确到)2,2(xx)1.0 （ 2 ）若 ，求 ]2,0[xx3. 反正切的概念 在开区间 内 , 符合条 件 ( 为任意实数 ) 的角 , 叫做实数 的反正切 ,记作 : , 即 其中 且 .,22tan xaaxaarctan aarctanxa,2 2x  tanax例 5.(1) 已知 : , 且 , 求(2) 已知 : , 且 , 求 的取值集合 . cot2x ,2 2x  xxcot2x 0,2练习 :课本 76 页 2(3)(6)3(2)(4)练习 1 、求适合下列条件的角 x练习 2 、求适合下列条件的 x 的集合 1 、已知任意一个角 ( 角必须属于所涉及的三角函数的定义域 ) 可以求...