初三数学函数的解析式课件 华东师大版 课件VIP免费

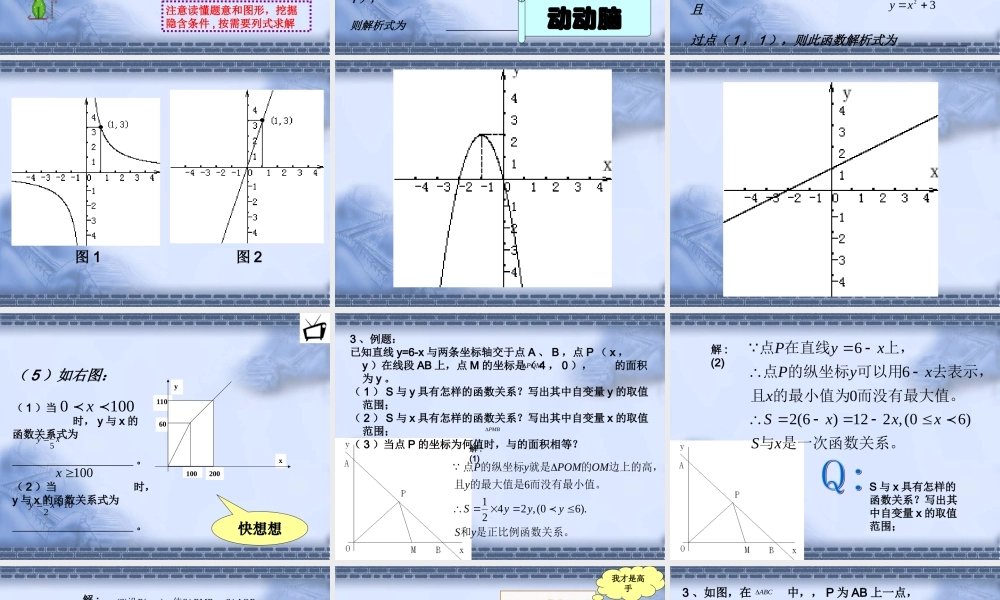
一、求函数的解析式的方法：（ 1 ）待定系数法：先根据函数的类型，作出假设，设出式子中的未知系数，再根据条件求出未知系数，从而写出这个式子。（ 2 ） 图象信息法：根据图象中给出的信息，寻找相关的条件求解。（ 3 ） 题意与图形结合法：注意读懂题意和图形，挖掘隐含条件，按需要列式求解。 kxy )0( kA. 求正比例函数的解析式 :只需要知道这个正比例函数经过某一点 ( 这点不能是原点 )B. 求一次函数的解析式 :)0( kbkxyC. 求反比例函数的解析式：需要知道两个独立的条件)0( kxky需要知道反比例函数经过某一点 D. 求二次函数的解析式cbxaxy2khxay2)())((21xxxxay需要知道二次函数经过某三点需要知道二次函数的定点及它经过的某一点需要知道抛物线及与 X轴的焦交点及它经过的某一点 根据图像中给出的信息，寻找相关条件求解注意读懂题意和图形，挖掘隐含条件 , 按需要列式求解 二、练习 1 ：（ 1 ）、若正比例函数 的图象经过（ -9 ， 2 ），则正比例函数的解析式是 。（ 2 ）、若 y 与 x 成反比例，当时 ， ，则 y 与 x的函数解析式是 。（ 3 ）、若一次函数的图象经过点 A （ 1 ， -3 ）， B （ 3 ，1 ），则解析式为 。kxy 51xxy92xy315y52  xy动动脑 （ 4 ）一次函数 的图象经过点（ 2 ， 1 ）且平行于直线，这个一次函数的解析式为 。（ 5 ）写出一个过点（ 0 ， 3 ）的函数的解析式 ____________________ 。（ 6 ）设二次函数图象的顶点坐标为（ 1 ， 3 ），且过点（ 1 ， 1 ），则此函数解析式为 。bkxy32  xy3)3(812 xy32 xy 图 1图 2 （ 5 ）如右图：（ 1 ）当 时， y 与 x 的函数关系式为 。（ 2 ）当 时，y 与 x 的函数关系式为 。x11060100200yxy531021 xy1000x100x快想想 3 、例题：已知直线 y=6-x 与两条坐标轴交于点 A 、 B ，点 P （ x ，y ）在线段 AB 上，点 M 的坐标是（ 4 ， 0 ）， 的面积为 y 。（ 1 ） S 与 y 具有怎样的函数关系？写出其中自变量 y 的取值范围；（ 2 ） S 与 x 具有怎样的函数关系？写出其中自变量 x 的取值范围；（ 3 ）当点 P 的坐标为何值时，与的面积相等？是正比例函数关系。和而没有最小值。的最大值是且边上的高，的就是的纵...