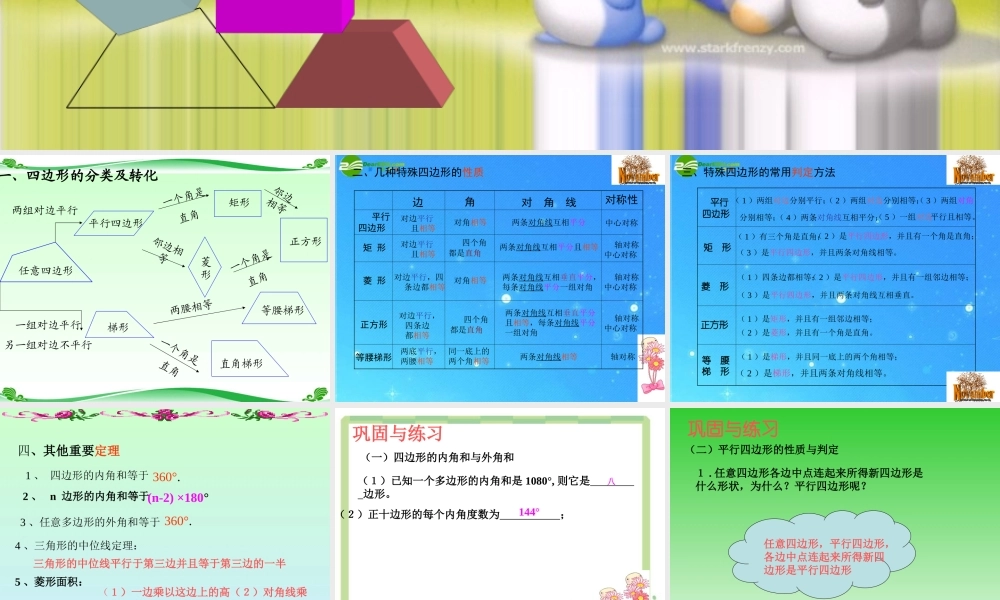
W 任意四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形两组对边平行一个角是直角邻边相等邻边相等一个角是直角一个角是直角两腰相等一组对边平行另一组对边不平行一、四边形的分类及转化 二、几种特殊四边形的性质 平行四边形矩 形菱 形正方形等腰梯形边对边平行 且相等对边平行 且相等对边平行,四 条边都相等对边平行, 四条边 都相等两底平行,两腰相等角对角相等 四个角都是直角对角相等 四个角都是直角同一底上的两个角相等对 角 线两条对角线互相平分两条对角线互相平分且相等两条对角线互相垂直平分,每条对角线平分一组对角两条对角线互相垂直平分且相等,每条对角线平分一组对角两条对角线相等对称性中心对称 轴对称中心对称 轴对称中心对称 轴对称中心对称轴对称 三、特殊四边形的常用判定方法 平行 四边形( 1 )两组对边分别平行;( 2 )两组对边分别相等;( 5 )一组对边平行且相等。( 4 )两条对角线互相平分;( 3 )两组对角矩 形( 1 )有三个角是直角;( 2 )是平行四边形,并且有一个角是直角;( 3 )是平行四边形,并且两条对角线相等。 菱 形( 1 )四条边都相等;( 2 )是平行四边形,并且有一组邻边相等;( 3 )是平行四边形,并且两条对角线互相垂直。正方形( 1 )是矩形,并且有一组邻边相等;( 2 )是菱形,并且有一个角是直角。等 腰梯 形( 1 )是梯形,并且同一底上的两个角相等;( 2 )是梯形,并且两条对角线相等。分别相等; 1 、 四边形的内角和等于 四、其他重要定理2 、 n 边形的内角和等于3 、任意多边形的外角和等于360°.4 、三角形的中位线定理: 360°.(n-2) ×180°三角形的中位线平行于第三边并且等于第三边的一半5 、菱形面积: (1)一边乘以这边上的高(2)对角线乘积的一半 巩固与练习(一)四边形的内角和与外角和(1)已知一个多边形的内角和是 1080°, 则它是 边形。 (2)正十边形的每个内角度数为 ;八 144° 1 . 任意四边形各边中点连起来所得新四边形是什么形状,为什么?平行四边形呢?任意四边形,平行四边形,各边中点连起来所得新四边形是平行四边形巩固与练习(二)平行四边形的性质与判定 2 . 已知:平行四边形ABCD的两条对角线AC与BD相交于点O,E、 F 是BD上的两个点, 若 BE=DF 求证:四边形AECF是平行四边形ABCDEFO 畅谈收获通过本节课的学习,谈谈你的收获? Listen and say the months in a year.