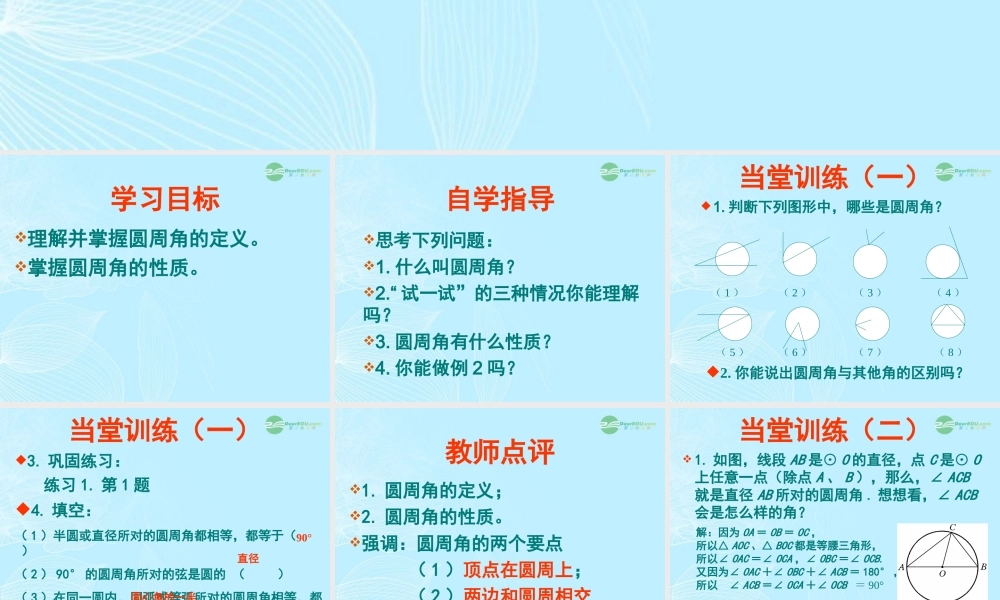
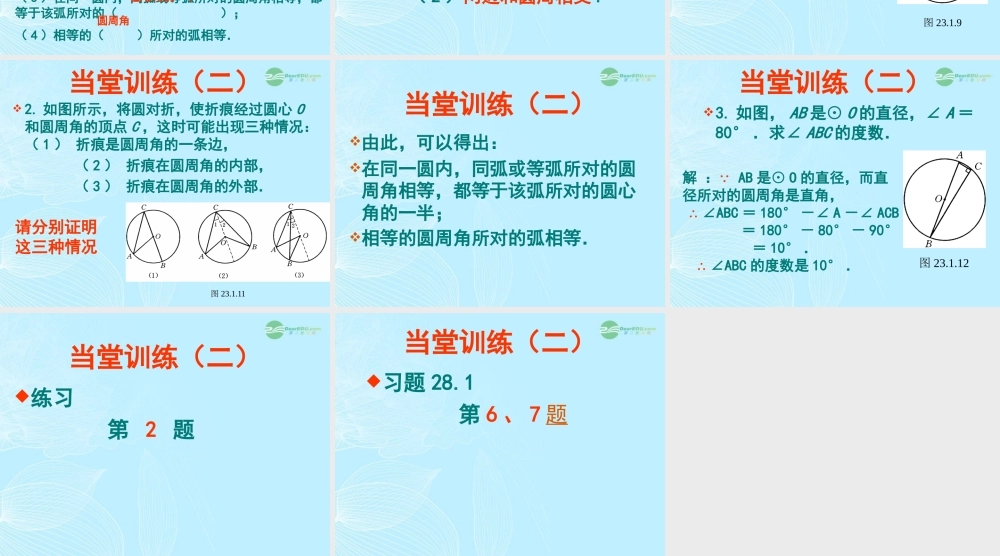
28.1.3 圆的认识——圆周角(1)学习目标理解并掌握圆周角的定义。掌握圆周角的性质。自学指导思考下列问题:1. 什么叫圆周角?2.“ 试一试”的三种情况你能理解吗?3. 圆周角有什么性质?4. 你能做例 2 吗?当堂训练(一)1. 判断下列图形中,哪些是圆周角?( 1 )( 5 )( 6 )( 4 )( 3 )( 2 )( 7 )( 8 )2. 你能说出圆周角与其他角的区别吗?当堂训练(一)3. 巩固练习: 练习 1. 第 1 题4. 填空:( 1 )半圆或直径所对的圆周角都相等,都等于( ) ( 2 ) 90° 的圆周角所对的弦是圆的 ( )( 3 )在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的( ); ( 4 )相等的( )所对的弧相等. 90° 直径 圆心角的一半 圆周角 教师点评1. 圆周角的定义;2. 圆周角的性质。强调:圆周角的两个要点 ( 1 )顶点在圆周上; ( 2 )两边和圆周相交 .当堂训练(二) 1. 如图,线段 AB 是⊙ O 的直径,点 C 是⊙ O上任意一点(除点 A 、 B ),那么,∠ ACB就是直径 AB 所对的圆周角 . 想想看,∠ ACB会是怎么样的角? 图 23.1.9 解:因为 OA = OB = OC ,所以△ AOC 、△ BOC 都是等腰三角形, 所以∠ OAC =∠ OCA ,∠ OBC =∠ OCB.又因为∠ OAC +∠ OBC +∠ ACB = 180° ,所以 ∠ ACB =∠ OCA +∠ OCB = 90° 当堂训练(二) 2. 如图所示,将圆对折,使折痕经过圆心 O和圆周角的顶点 C ,这时可能出现三种情况:( 1 ) 折痕是圆周角的一条边, ( 2 ) 折痕在圆周角的内部, ( 3 ) 折痕在圆周角的外部. 图 23.1.11 请分别证明这三种情况当堂训练(二)由此,可以得出:在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等. 当堂训练(二)3. 如图, AB 是⊙ O 的直径,∠ A =80° .求∠ ABC 的度数. 图 23.1.12 解 :∵ AB 是⊙ O 的直径,而直径所对的圆周角是直角, ∴ ∠ABC = 180° -∠ A -∠ ACB = 180° - 80° - 90° = 10° . ∴ ∠ABC 的度数是 10° .当堂训练(二)练习 第 2 题当堂训练(二)习题 28.1 第 6 、 7 题