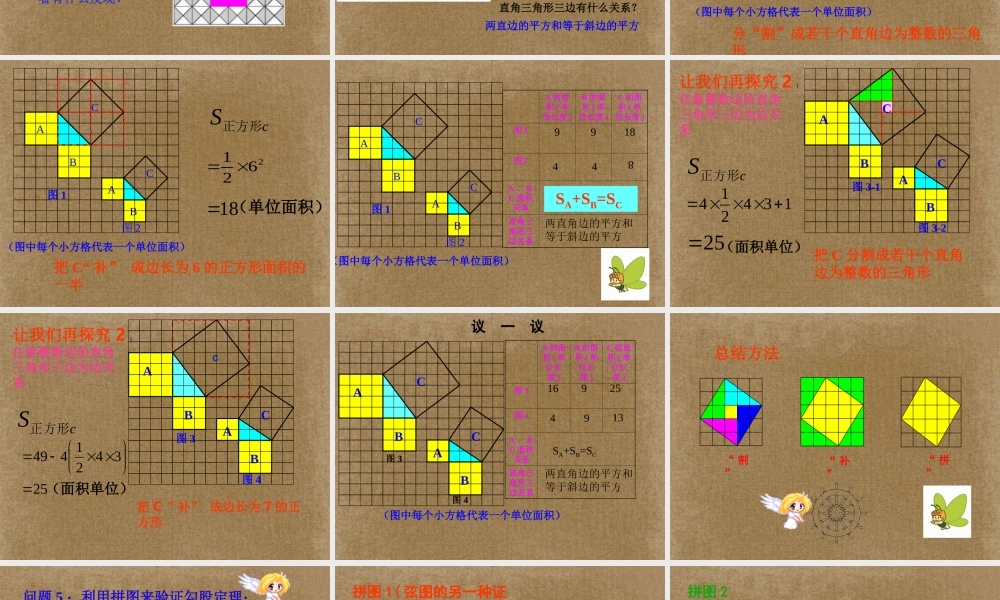
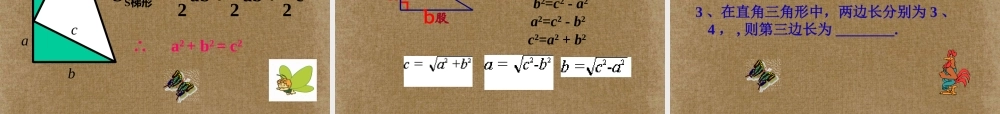18.1 勾股定理勾股弦 千古第一定理祝同学们学习快乐这就是本届大会会徽的图案.问题 1你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.1955 年希腊发行的一枚纪念一位数学家的邮票问题 2问题 3 相传 2500 年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?毕达哥拉斯(公元前 572-前 492 年),古希腊著名的哲学家、数学家、天文学家 . 数学家毕达哥拉斯的发现:A 、 B 、 C 的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方ABCABCABC(图中每个小方格代表一个单位面积)图 1图 2cS正方形143 3182 分“割”成若干个直角边为整数的三角形(单位面积)问题 4让我们一起探究 1 :等腰直角三角形三边关系ABCABC(图中每个小方格代表一个单位面积)图 1图 2cS正方形216218 (单位面积)把 C“ 补” 成边长为 6 的正方形面积的一半ABCABC(图中每个小方格代表一个单位面积)图 1图 2 SA+SB=SCA 的面积 ( 单位长度 )B 的面积 ( 单位长度 )C 的面积 ( 单位长度 )图 19918图 2A 、 B 、C 面积关系直角三角形三边关系448两直角边的平方和等于斜边的平方ABC图 3-1ABC图 3-2把 C 分割成若干个直角边为整数的三角形cS正方形25144 3 12 (面积单位)让我们再探究 2 :任意整数边的直角三角形三边为边关系把 C“ 补” 成边长为 7 的正方形cS正方形cAB图 3ABC图 4让我们再探究 2 :任意整数边的直角三角形三边为边关系253421449(面积单位)ABC图 3ABC图 4A 的面积 ( 单位长度 )B 的面积 ( 单位长度 )C 的面积 ( 单位长度 )图 3图 4A 、 B 、C 面积关系直角三角形三边关系议 一 议169254913SA+SB=SC两直角边的平方和等于斜边的平方(图中每个小方格代表一个单位面积)“ 割”“ 补”“ 拼”总结方法问题 5 :利用拼图来验证勾股定理:cab1 、准备四个全等的直角三角形(设直角三角形的两条直角边分别为 a , b ,斜边c );2 、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看3 、你拼的正方形中是否含有以斜边 c 为边的正方形?4 、你能否就你拼出的图说明...