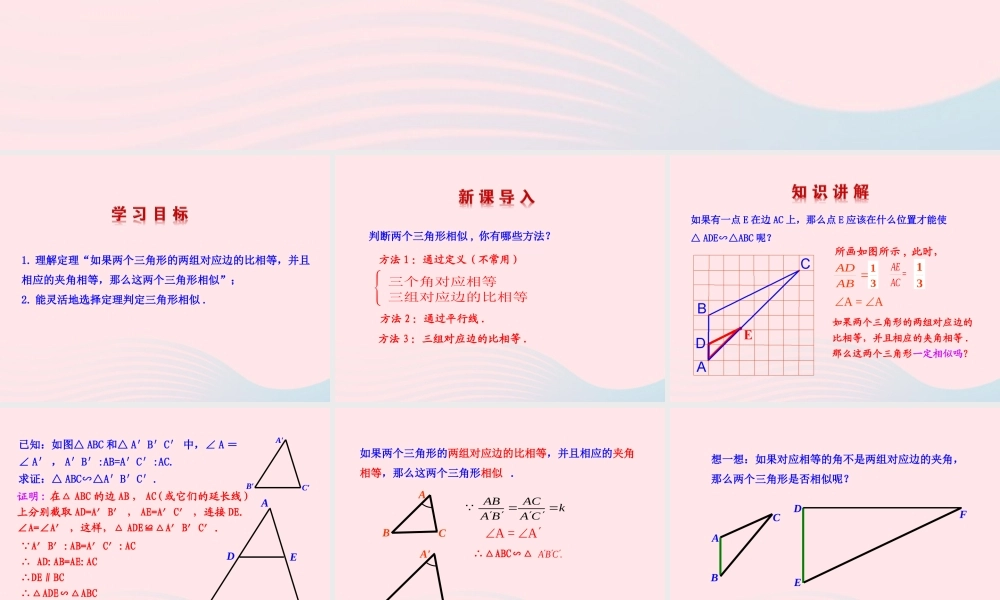
27.2.1 相似三角形的判定第 3 课时1. 理解定理“如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似”;2. 能灵活地选择定理判定三角形相似 .判断两个三角形相似 , 你有哪些方法?方法 1 :通过定义(不常用)三个角对应相等三组对应边的比相等方法 2 :通过平行线 .方法 3 :三组对应边的比相等 .如果有一点 E 在边 AC 上,那么点 E 应该在什么位置才能使△ ADE∽△ABC 呢? ADAB所画如图所示 , 此时,如果两个三角形的两组对应边的比相等,并且相应的夹角相等 .那么这两个三角形一定相似吗? A = A=AEAC3131A′B′C′ABCED证明 : 在△ ABC 的边 AB , AC( 或它们的延长线 )上分别截取 AD=A′B′ , AE=A′C′ ,连接 DE.∠A=∠A′ ,这样,△ ADE≌△A′B′C′. A′B′:AB=A′C′:AC ∴ AD:AB=AE:AC∴DE∥BC∴△ADE∽△ABC∴△A′B′C′∽△ABC已知:如图△ ABC 和△ A′B′C′ 中,∠ A =∠ A′ , A′B′:AB=A′C′:AC.求证:△ ABC∽△A′B′C′.∴△ABC∽△. A B C如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似 . ABACkA BA CA = A ABCA′B′C′想一想:如果对应相等的角不是两组对应边的夹角,那么两个三角形是否相似呢?ABCDEF下列各组条件中不一定使△ ABC 与△ DEF 相似的是( )A.∠A=∠D=40° ∠B=∠E=60°AB=DEB.∠A=∠D=60° ∠B= 40° ∠E=80° C.∠A=∠D=50° AB=3 AC=5 DE=6 DF=10 D.∠B=∠E=70° AB : DE=AC : DF 注意:对应相等的角必须是两组对应边的夹角,如果不是夹角,则它们不一定会相似.D【跟踪训练】1 .(烟台 · 中考)如图,△ ABC 中,点 D 在线段 BC 上,且△ ABC∽△DBA ,则下列结论一定正确的是( )A.AB2=BC·BD B.AB2=AC·BD C.AB·AD=BD·BC D.AB·AD=AD·CDABDCA2 .(吉林 · 中考)如图,在△ABC 中,∠ C=90° , D 是 AC 上一点,DE⊥AB 于点 E ,若 AC=8 , BC=6 , DE=3 ,则 AD 的长为( )A . 3 B . 4 C . 5 D . 6C3. (无锡 · 中考)如图,四边形 ABCD 的对角线 AC,BD 相交于 O ,且将这个四边形分成①、②、③、④四个三角形.若 OA : OC=0B : OD ,则下列结论中一定正确的是 ( ) .A .①与②相似 B .①...