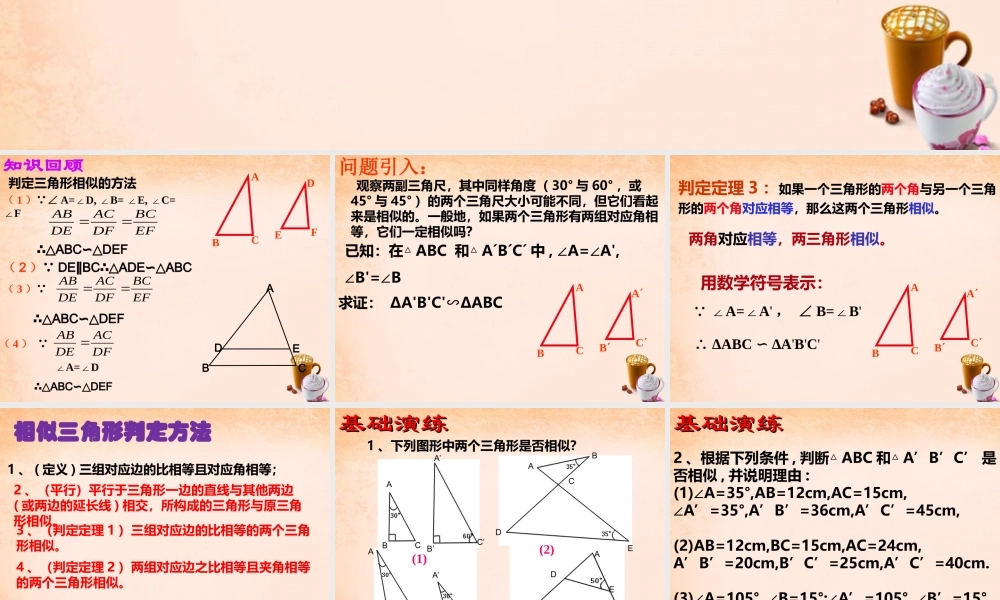
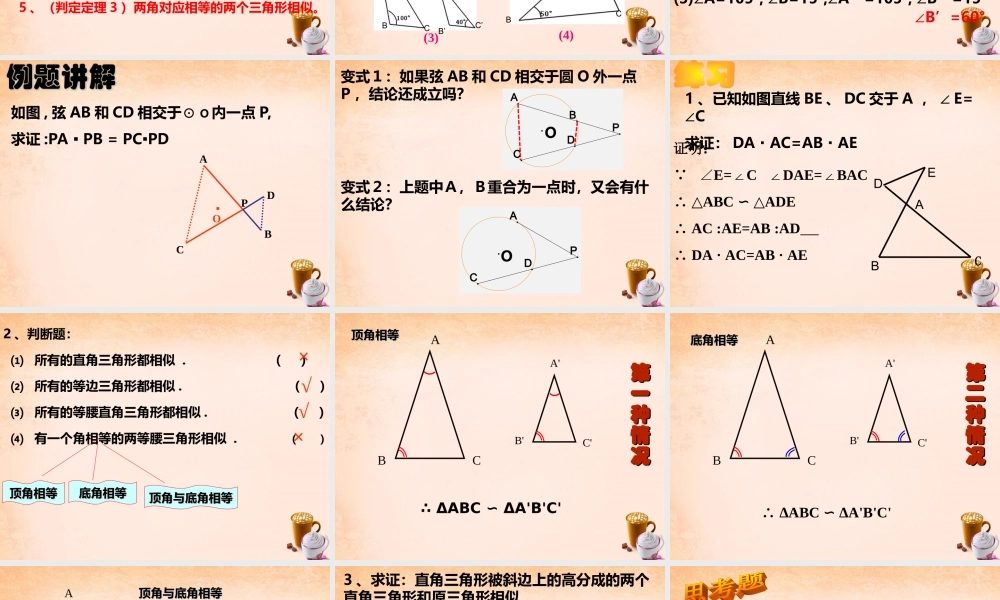
DBACE( 2 ) DE BCADEABC∥∴△∽△判定三角形相似的方法知识回顾ACBEDF( 1 ) ∠ A=D, B= E, C= ∠∠∠∠F∠EFBCDFACDEAB∴△ABCDEF∽△EFBCDFACDEAB( 3 ) ∴△ABCDEF∽△( 4 ) DFACDEAB ∠A=D∠∴△ABCDEF∽△问题引入: 观察两副三角尺,其中同样角度( 30° 与 60° ,或45° 与 45° )的两个三角尺大小可能不同,但它们看起来是相似的。一般地,如果两个三角形有两组对应角相等,它们一定相似吗? 求证: ΔA'B'C'∽ΔABC已知:在△ ABC 和△ A´B´C´ 中 , ∠A=∠A',∠B'=∠BACBB´A´C´ ∠A=A∠ ' , ∠ B=B∠ ' ∴ ΔABC ΔA∽'B'C'用数学符号表示:判定定理 3 :如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。两角对应相等,两三角形相似。ACBB´A´C´相似三角形判定方法1 、 ( 定义 ) 三组对应边的比相等且对应角相等;3 、(判定定理 1 )三组对应边的比相等的两个三角形相似。2 、(平行)平行于三角形一边的直线与其他两边( 或两边的延长线 ) 相交,所构成的三角形与原三角形相似。4 、(判定定理 2 )两组对应边之比相等且夹角相等的两个三角形相似。5 、(判定定理 3 )两角对应相等的两个三角形相似。ABCA’B’C’基础演练基础演练1 、下列图形中两个三角形是否相似?ABCDEABCA’C’B’ABCDE(1)(2)(3)(4)2 、根据下列条件 , 判断△ ABC 和△ A’B’C’ 是否相似 , 并说明理由 :(1)∠A=35°,AB=12cm,AC=15cm,∠A’=35°,A’B’=36cm,A’C’=45cm,(2)AB=12cm,BC=15cm,AC=24cm,A’B’=20cm,B’C’=25cm,A’C’=40cm.(3)∠A=105°, ∠B=15°;∠A’=105°, ∠B’=15°基础演练基础演练 ∠B’=60°如图 , 弦 AB 和 CD 相交于⊙ O 内一点 P, 求证 :PA ▪ PB = PC▪PDO▪DPCBA变式1:如果弦 AB 和 CD 相交于圆 O 外一点P ,结论还成立吗?DBPAC变式2:上题中A,B重合为一点时,又会有什么结论?DPACOO1 、已知如图直线 BE 、 DC 交于 A , ∠ E= ∠C求证: DA·AC=AB·AEDEABC证明: ∠E=C DAE=BAC ∠∠∠ ∴ △ABC ADE∽ △ ∴ AC :AE=AB :AD ∴ DA · AC=AB · AE2 、判断题: ⑴ 所有的直角三角形都相似 . ( ) ⑵ 所有的等边三角形都相似 . ( ) ⑶ 所有的等腰直角三角形都相似 . ( ) ⑷ 有一个角相等...