数学 3.1.1两角和与差的余弦课件 新人教B版必修4 课件VIP免费

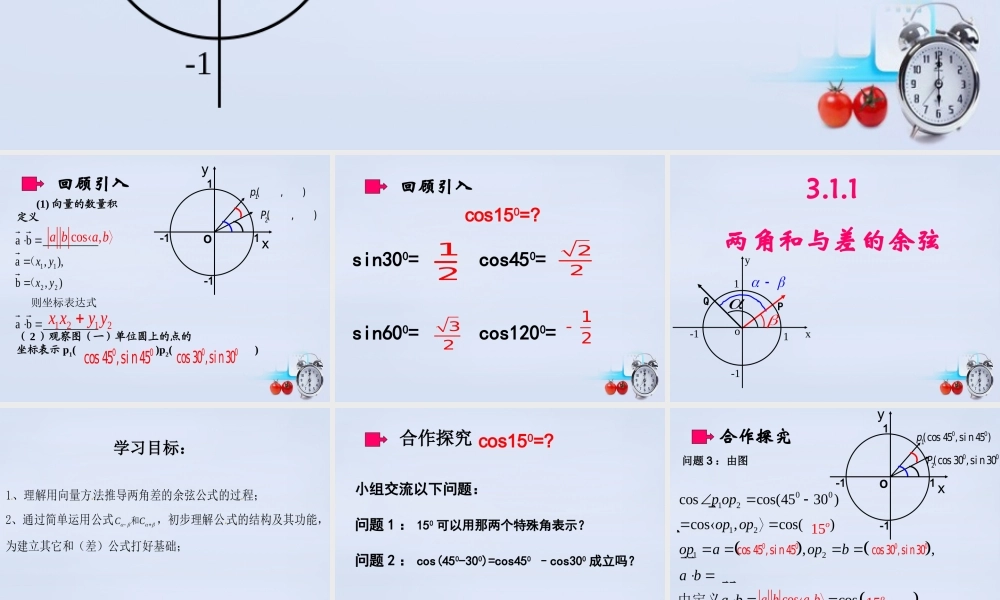
3.1.1两角和与差的余弦PQ1y-11-1xo__________ba),,a11 yx（),b22 yx（__________ba(1) 向量的数量积定义 则坐标表达式 （ 2 ）观察图（一）单位圆上的点的坐标表示 p1( )p2( )xyo2(,)P1(,)p-1-111回顾引入cos,a ba b1 212x xy y00cos30 ,si n3000cos 45 ,si n45sin300= cos450=sin600= cos1200= 1222321- 2cos150=?回顾引入3.1.1两角和与差的余弦PQ1y-11-1xo学习目标：1、理解用向量方法推导两角差的余弦公式的过程； 2、通过简单运用公式CC  和，初步理解公式的结构及其功能， 为建立其它和（差）公式打好基础； cos150=?问题 1 ： 150 可以用那两个特殊角表示？问题 2 ： cos(450-300)=cos450 –cos300 成立吗？合作探究 小组交流以下问题：合作探究xyo002(cos 30 ,si n30 )P001(cos 45 ,si n45 )p-1-111问题 3 ：由图 0012121200coscos(4530 )cos,cos(),,coscos(4530 )p opop opopaopba ba b     ��由定义所以15o00cos 45 ,si n4500cos 30 ,si n30cos,a ba b15o cos 45 cos 30si n45 si n30 0cos15cos 45 cos 30si n45 si n30xyo00(cos 30 ,si n30 )P00Q(cos 45 ,si n45 )-1-111合作探究问题 4 ：由出发，你能推广到对任意的两个角都成立吗？如何推导？公式推导观看微课sinsincoscos)-cos(两角差的余弦公式两角和的余弦公式 ？cos( + )cos cos -si n si n 2 、公式中两边的符号正好相反3 、式子右边同名三角函数相乘再加减， 且余弦在前正弦在后。公式理解-bb用代替注意注意 ::11 、 可取任意角。、 可取任意角。、 )cos(sinsincoscosC两角和与差的余弦公式余余正正 , 符号反结构特点：第一关：小试身手请用特殊角分别代替公式中 α 、 β ，你能求哪些非特殊角的值呢？（选择的特殊角可以是 30°60°45°等）请每组自行选择两个特殊角计算和与差的余弦 四、小组交流合作，公式应用闯关 四． 互相交流，小组活动 公式应用闯关 2π,π(1)cos()___________(2)cos()___________(3)cos()__________(4)cos()__________...