九年级数学下册 第二十六章 反比例函数261 反比例函数2613 二次函数ya(x h)2k的图象第2课时课件 (新版)新人教版 课件VIP免费

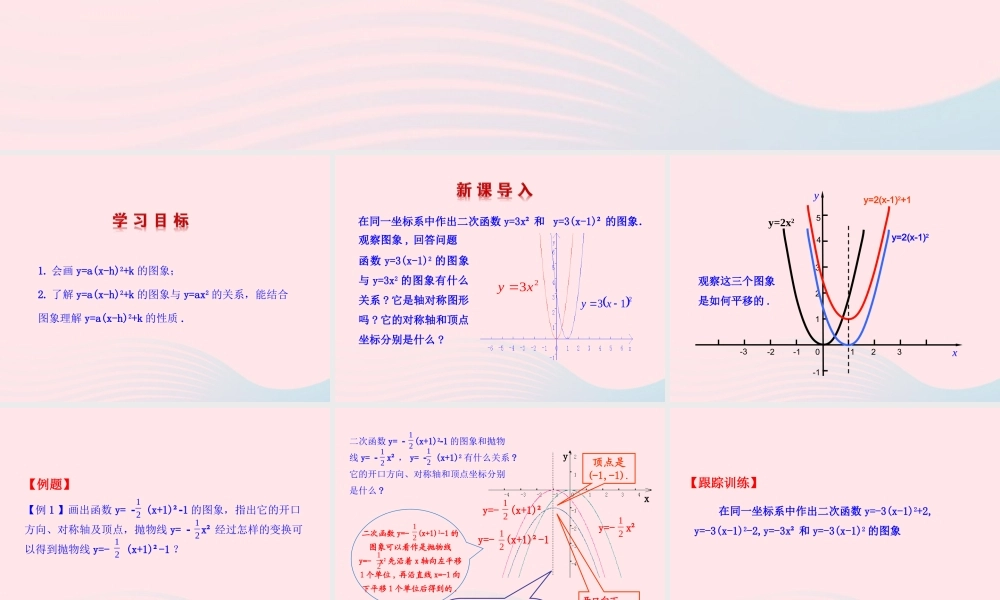
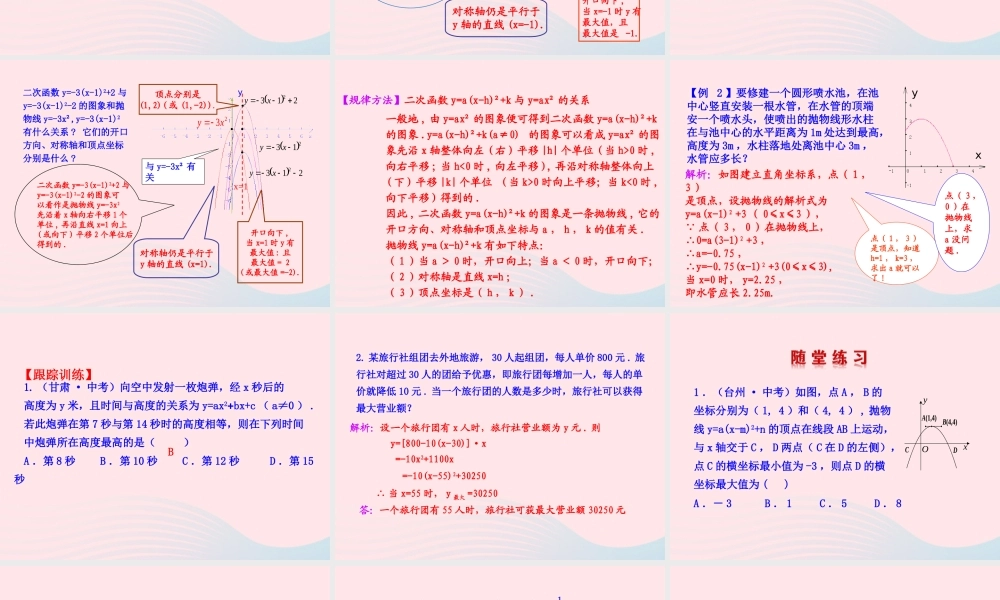
26.1.3 二次函数 y=a(xh)2+k 的图象第 2 课时1. 会画 y=a(x-h)2+k 的图象；2. 了解 y=a(x-h)2+k 的图象与 y=ax2 的关系，能结合图象理解 y=a(x-h)2+k 的性质 .观察图象 , 回答问题函数 y=3(x-1)2 的图象与 y=3x2 的图象有什么关系 ? 它是轴对称图形吗 ? 它的对称轴和顶点坐标分别是什么 ? 23xy 213xy在同一坐标系中作出二次函数 y=3x² 和 y=3(x-1)² 的图象． 123-1-2-301234-1xy5y=2(x-1)2+1y=2(x-1)2 y=2x2观察这三个图象是如何平移的 .【例 1 】画出函数 y=  (x+1)²1 的图象，指出它的开口方向、对称轴及顶点，抛物线 y=  x² 经过怎样的变换可以得到抛物线 y=- (x+1)²-1 ？121212【例题】二次函数 y=- (x+1)2-1 的图象可以看作是抛物线y=- x2 先沿着 x 轴向左平移1 个单位 , 再沿直线 x=-1 向下平移 1 个单位后得到的 .二次函数 y=  (x+1)21 的图象和抛物线 y=  x² ， y=  (x+1)2 有什么关系 ?它的开口方向、对称轴和顶点坐标分别是什么 ?对称轴仍是平行于y 轴的直线 (x=-1). 顶点是(-1,-1).开口向下 ,当 x=-1 时 y 有最大值，且最大值是 -1.yx1212121212y=- (x+1)²12y=- x²y=- (x+1)²-11212 在同一坐标系中作出二次函数 y=-3(x-1)2+2, y=-3(x-1)2-2,y=-3x² 和 y=-3(x-1)2 的图象【跟踪训练】2132 xy对称轴仍是平行于y 轴的直线 (x=1). 顶点分别是(1,2)( 或 (1,-2)).二次函数 y=-3(x-1)2+2 与y=-3(x-1)2-2 的图象可以看作是抛物线 y=-3x2先沿着 x 轴向右平移 1 个单位 , 再沿直线 x=1 向上( 或向下 ) 平移 2 个单位后得到的 .213xy开口向下 ,当 x=1 时 y 有最大值 : 且最大值 = 2( 或最大值 =-2).2132 xyy23xyx=1与 y=-3x² 有关二次函数 y=-3(x-1)2+2 与y=-3(x-1)2-2 的图象和抛物线 y=-3x²,y=-3(x-1)2有什么关系 ? 它们的开口方向、对称轴和顶点坐标分别是什么 ?【规律方法】二次函数 y=a(x-h)²+k 与 y=ax² 的关系一般地 , 由 y=ax² 的图象便可得到二次函数 y=a(x-h)²+k的图象 .y=a(x-h)²+k(a≠0) 的图象可以看成 y=ax² 的图象先沿 x 轴整体向左 ( 右 ) 平移 |h| 个单位 ( 当 h>0 时 ,向右平移 ; 当 h<0 时 , 向左平移 ), 再沿对称轴整体向上( 下 ) 平移 |k| 个单...