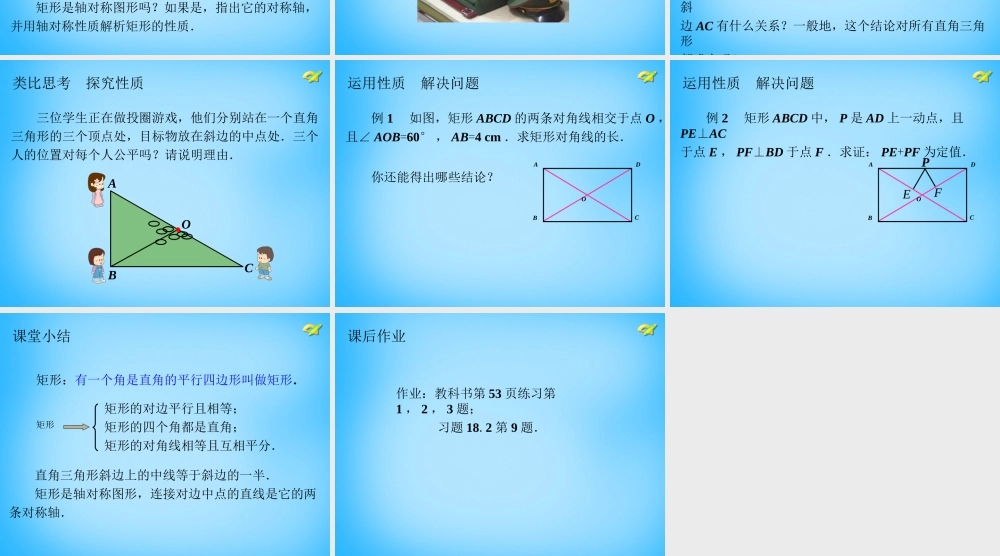
18.2.1 矩形( 1 )• 本课是在学习了平行四边形后,通过角的特殊化引 入了矩形的概念,并研究矩形的性质,得到直角三 角形斜边上的中线的性质定理.课件说明• 学习目标: 1 .理解矩形的概念,明确矩形与平行四边形的区别 与联系; 2 .探索并证明矩形的性质,会用矩形的性质解决简 单的问题; 3 .探索并掌握“直角三角形斜边上的中线等于斜边 的一半”这个定理.• 学习重点: 矩形区别于一般平行四边形的性质的探索、证明和应 用.课件说明独木桥 当独木桥前后运动时,四边形 ABCD 是什么形状?当独木桥最后停下时,四边形 ABCD 有什么特殊的变化?当独木桥静止时,四边形 ABCD 是什么图形?观察思考 形成概念 有一个角是直角 的平行四边形叫做矩 形. 小学中学习过的长方形是矩形吗?正 方形是矩形吗?ABCD 你能分别证明这些猜想吗? 矩形是轴对称图形吗?如果是,指出它的对称轴,并用轴对称性质解析矩形的性质.类比思考 探究性质 作为特殊的平行四边形,矩形具有平行四边形所有的性质.此外,矩形还有哪些一般平行四边形没有的特殊性质呢?B C D A O O B C D A 类比思考 探究性质 为什么矩形的被子和床单可以反复折叠仍然是矩形?请你用一张矩形纸片做模拟实验,并说明原因 .A B C D O 类比思考 探究性质 如图,一张矩形纸片,沿着对角线剪去一半,你能得到什么结论?B C O A Rt△ABC 中, BO 是一条怎样的线段?它的长度与斜边 AC 有什么关系?一般地,这个结论对所有直角三角形都成立吗? 类比思考 探究性质 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗?请说明理由.A B C O 你还能得出哪些结论?运用性质 解决问题 例 1 如图,矩形 ABCD 的两条对角线相交于点 O ,且∠ AOB=60° , AB=4 cm .求矩形对角线的长.A B C D O 运用性质 解决问题 例 2 矩形 ABCD 中, P 是 AD 上一动点,且PE⊥AC于点 E , PF⊥BD 于点 F .求证: PE+PF 为定值.A B C D O P E F 直角三角形斜边上的中线等于斜边的一半. 矩形是轴对称图形,连接对边中点的直线是它的两条对称轴. 课堂小结 矩形 矩形的对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分.矩形:有一个角是直角的平行四边形叫做矩形.作业:教科书第 53 页练习第1 , 2 , 3 题; 习题 18.2 第 9 题.课后作业