八年级数学下册：10.4探索三角形相似的条件(第2课时)课件 苏科版 课件VIP免费

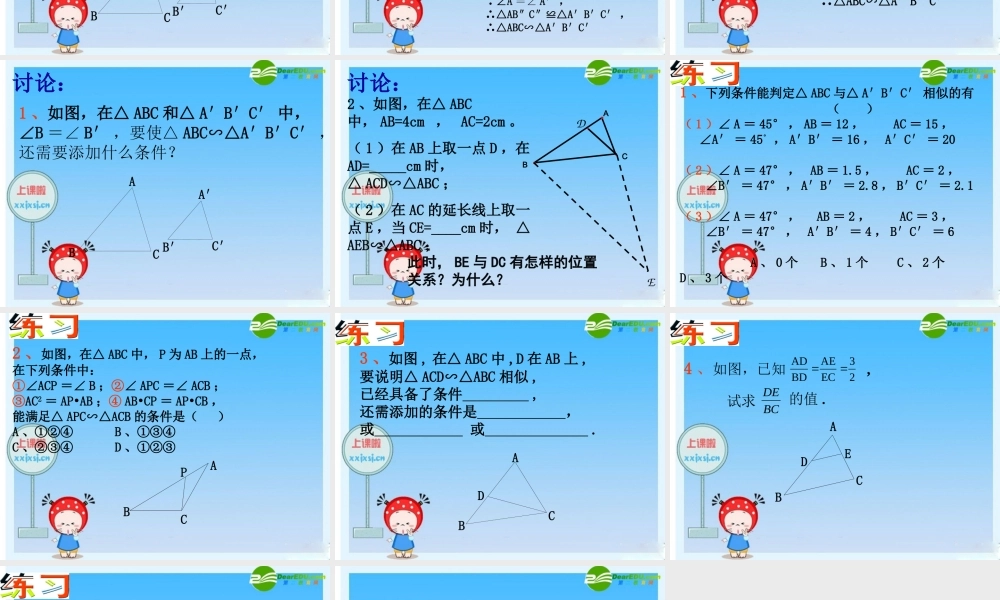
10.4 探索三角形相似的条件 (2)10.4 探索三角形相似的条件 (2) 1 、如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。2 、平行于三角形一边的直线与其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。回顾：三角形相似的条件 情境创设： 当两个三角形的两条边及其夹角对应相等时，这两个三角形全等。相应地，我们探索两个三角形相似，可以从哪几个方面考虑找出条件？ 1 、如图，在△ ABC 和△ A′B′C′ 中，∠ A ＝∠ A′ ，,比较∠ B 和∠ B′ 的大小 . 由此，你能判断△ABC 和△ A′B′C′ 相似吗？为什么？ 2CAACBAABABCA′B′C′ KCAACBAAB2 、在上题的条件下，设改变 k 的值的大小，（ ∠ A ＝∠ A′ 不变）再试一试，你能判断△ ABC 与△ A′B′C′ 相似吗？ABCA′B′C′B″C″ 'C'AAC'B'AAB CAACBAAB''''CAACBAAB 如图，在△ ABC 和△ A′B′C′ 中，∠ A ＝∠ A′ ， ，那么△ ABC∽△A′B′C′解：假设 AB ＞ A′B′ ，在 AB 上截取 AB″ ＝ A′B′ ，过点 B″作 B″C″∥BC ，交 AC 于点 C″ ，在△ ABC 和△ AB″C″ ， B″C″∥BC ∴△ABC∽△AB″C″ ， ∴ 又 AB″ ＝ A′B′ ，∴ AC″ ＝ A′C′ ， ∠A ＝∠ A′ ，∴△AB″C″≌△A′B′C′ ，∴△ABC∽△A′B′C′ABCA′B′C′B″C″ 由此得判定方法三：如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似。 几何语言： 在△ ABC 和△ A′B′C′ 中，∠A ＝∠ A′ ，'C'AAC'B'AAB ∴△ABC∽△A′B′C′ABCA′B′C′ 1 、如图，在△ ABC 和△ A′B′C′ 中，∠B ＝∠ B′ ，要使△ ABC∽△A′B′C′ ，还需要添加什么条件？ABCA′B′C′讨论： 2 、如图，在△ ABC中， AB=4cm ， AC=2cm 。（ 1 ）在 AB 上取一点 D ，在AD=_____cm 时， △ ACD∽△ABC ；（ 2 ）在 AC 的延长线上取一点 E ，当 CE=____cm 时， △AEB∽△ABC ；讨论：CBADE此时， BE 与 DC 有怎样的位置关系？为什么？ 1 、下列条件能判定△ ABC 与△ A′B′C′ 相似的有 （ ）（ 1 ）∠ A ＝ 45° ， AB ＝ 12 ， AC ＝ 15 ， ∠A′ ＝ 45° ， A′B′ ＝ 16 ， A′C′ ＝ 20 （ 2 ...