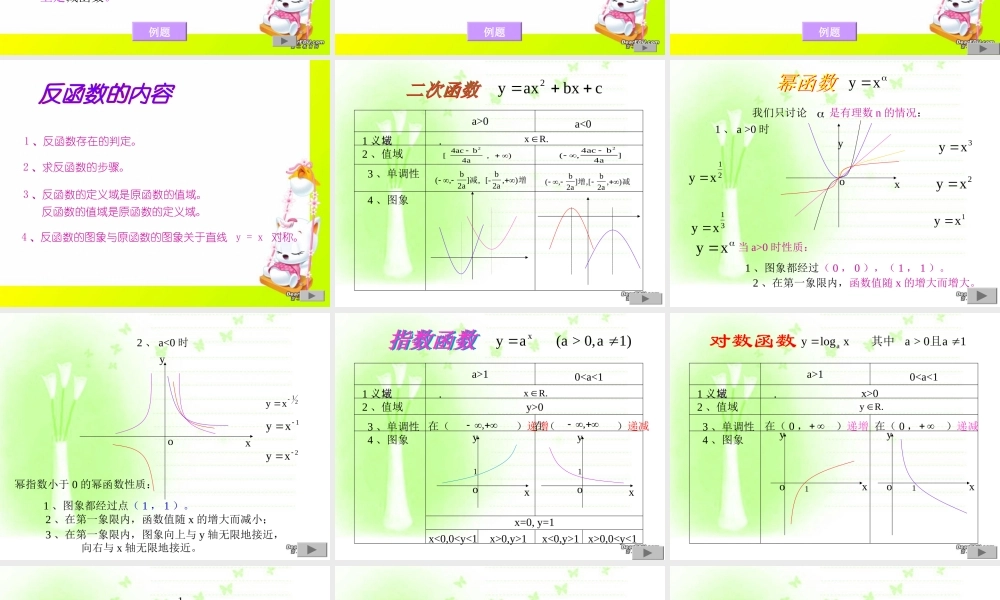
函数定义域奇偶性图象反函数值域单调性二次函数指数函数幂函数对数函数内容多怎么办?函数的复习主要抓住两条主线1 、函数的概念及其有关性质。2 、几种初等函数的具体性质。有办法!有办法!函数的概念函数的概念 A 、 B 是两个非空的集合,对于自变量 x 在定义域 A 内的任何一个值,在集合 B 中都有唯一的函数值 y 和它对应,自变量的值相当于原象,和它对应的函数值相当于象;函数值的集合 C 就是函数的值域。BCx1x2x3x4x5y1y2y3y4y5y6A函数的三要素:定义域,值域,对应法则。使函数有意义的 x 的取值范围。求定义域的主要依据 求定义域的主要依据1 、分母不为零。2 、偶数次的开方数大或等于零。3 、真数大于零。4 、底数大于零且不等于 1 。例题求值域的一些方法: 求值域的一些方法: 1 、公式法 2 、配方法3 、反函数法 4 、不等式法5 、判别式法 6 、换元法7 、数形结合法 8 、分离常数法9 、导数法 10 、利用函数单调性例题函数的单调性:函数的单调性: 如果对于属于这个区间的任意两个自变量的值 x1 , x2 , 当 x1 < x2 时,都有f (x1)f(x2) , 那么就说 f(x) 在这个区间上是减函数。例题一、函数的奇偶性定义一、函数的奇偶性定义前提条件:定义域关于原点对称。1 、奇函数 f (-x)= - f (x) 或 f (-x)+f (x) = 02 、偶函数 f (-x) = f (x) 或 f (-x) - f (x) = 0二、奇函数、偶函数的图象特点二、奇函数、偶函数的图象特点1 、奇函数的图象关于原点成中心对称图形。2 、偶函数的图象关于 y 轴成轴对称图形。例题函数的图象函数的图象1 、用描点法画图。2 、用某种函数的图象变形而成。( 1 )、关于 x 轴、 y 轴、原点、直线 y=x 的对称关系。( 2 )、平移关系。例题反函数的内容反函数的内容1 、反函数存在的判定。2 、求反函数的步骤。3 、反函数的定义域是原函数的值域。反函数的值域是原函数的定义域。4 、反函数的图象与原函数的图象关于直线 y = x 对称。二次函数 二次函数 yaxbxc21 、定义域 .2 、值域 xR .3 、单调性 4 、图象a>0a<0[,) 442acba (,] 442acba(,],,) ba2减增 [- b2a(,],[,) baba22增减...