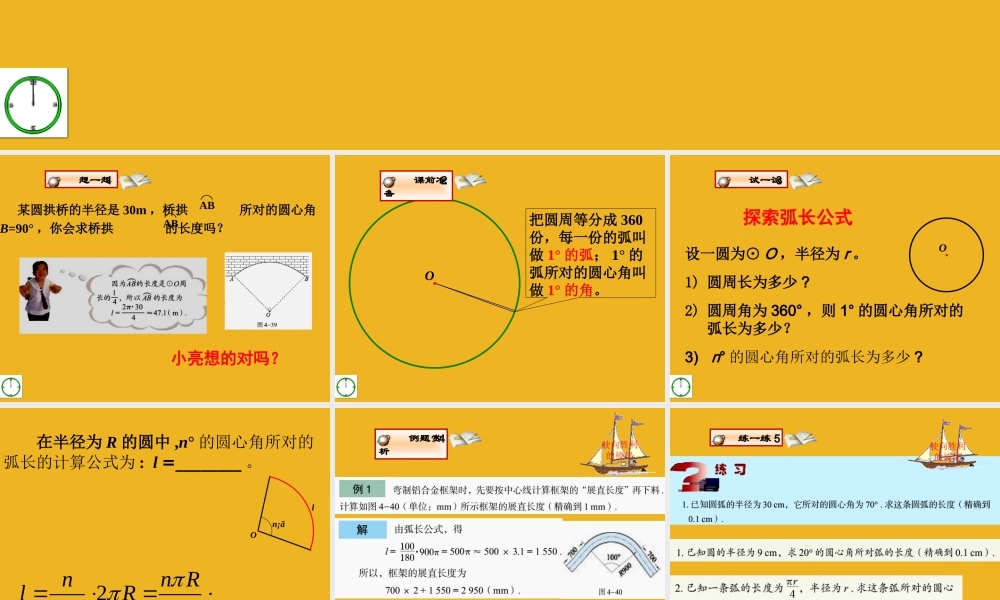
九年级数学 ( 上 ) 第四章: 对圆的进一步认识4.7 弧长及扇形面积的计算 某圆拱桥的半径是 30m ,桥拱 所对的圆心角∠AOB=90° ,你会求桥拱 的长度吗?AB⌒AB⌒小亮想的对吗? 想一想 11 O把圆周等分成 360份,每一份的弧叫做 1° 的弧; 1° 的弧所对的圆心角叫做 1° 的角。 课前准备 22 探索弧长公式设一圆为⊙ O ,半径为 r 。1) 圆周长为多少 ? 2) 圆周角为 360° ,则 1° 的圆心角所对的弧长为多少? 3) n° 的圆心角所对的弧长为多少 ?O 试一试 33 在半径为 R 的圆中 ,n° 的圆心角所对的弧长的计算公式为 : l =________ 。2360180nn RlRn¡ãlO 例题赏析 44驶向胜利的彼岸求弧长,你会了吗? 练一练 55驶向胜利的彼岸 练习 1: 如图 , 已知扇形的圆心角为 150°, 弧长为 20πcm, 求扇形的半径 .OAB练习 2: 如图 , 圆心角为 60° 的扇形的半径为10cm, 求这个扇形的周长 .OAB 练一练 66 挑战自我• 习题 4.7 1-2 题•祝你成功 ! 独立作业77驶向胜利的彼岸 结束寄语•形成天才的决定因素应该是勤奋 .下课了 ! 补充: 如图,某传送带的一个转动轮的半径为10cm. 1) 转动轮转一周 , 传送带上的物品 A 被传送多少厘米 ? 2) 转动轮转 1°, 传送带上的物品 A 被传送多少厘米 ? 3) 转动轮转 n°, 传送带上的物品 A 被传送多少厘米 ? 补充:制作弯形管道时 , 需要先按中心线计算“展直长度”再下料 , 试计算如图所示的管道的展直长度 , 即弧 AB 的长 .ABO