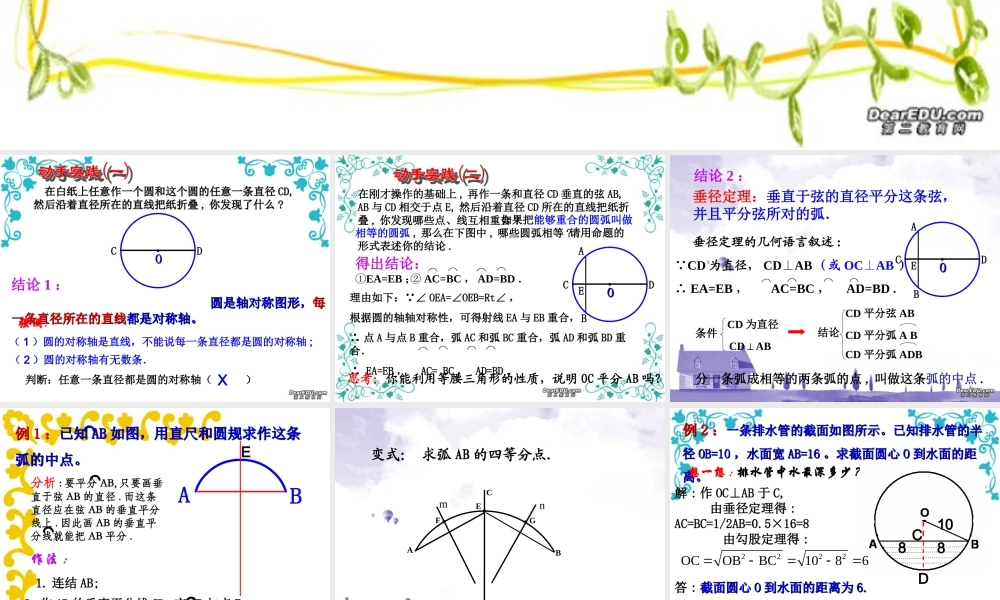
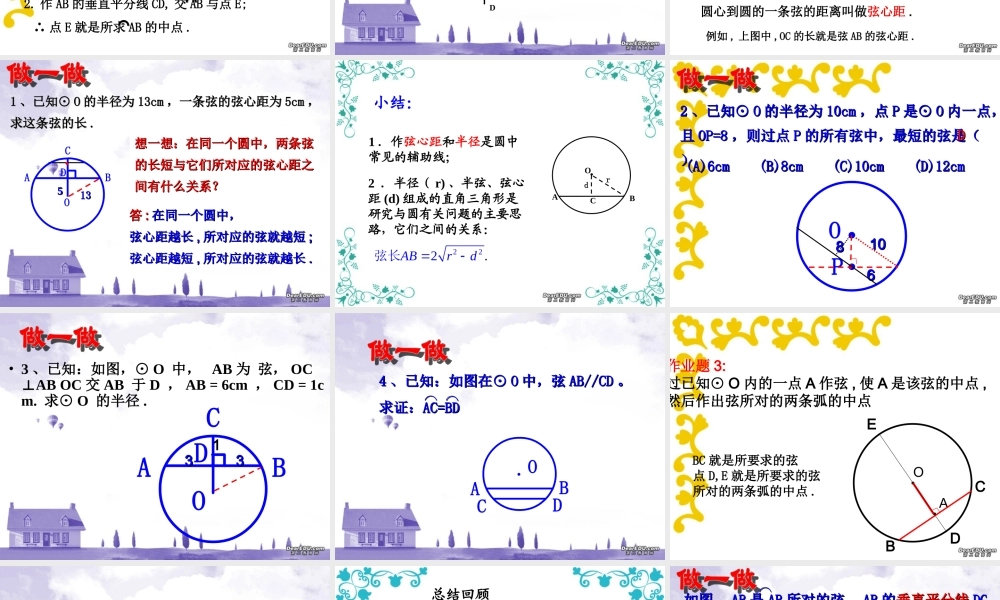
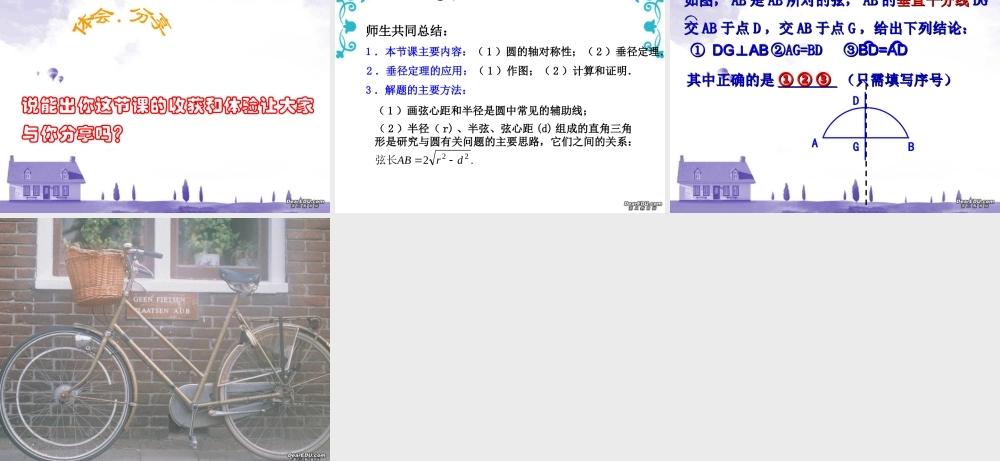
在白纸上任意作一个圆和这个圆的任意一条直径在白纸上任意作一个圆和这个圆的任意一条直径 CD, CD, 然后沿着直径所在的直线把纸折叠然后沿着直径所在的直线把纸折叠 ,, 你发现了什么你发现了什么 ??结论 1 : 圆是轴对称图形,圆是轴对称图形,每每一条直径所在的直线一条直径所在的直线都是对称轴。都是对称轴。强调:判断:任意一条直径都是圆的对称轴( )X( 1 )圆的对称轴是直线,不能说每一条直径都是圆的对称轴 ;( 2 )圆的对称轴有无数条.OOCD在刚才操作的基础上 , 再作一条和直径 CD 垂直的弦 AB,AB 与 CD 相交于点 E, 然后沿着直径 CD 所在的直线把纸折叠 , 你发现哪些点、、线互相重合 ? 如果把能够重合的圆弧叫做相等的圆弧 , 那么在下图中 , 哪些圆弧相等 ? 请用命题的形式表述你的结论 .ABE ② AC=BC , AD=BD .⌒⌒⌒⌒OOCD得出结论:①EA=EB ;理由如下: ∠ OEA=∠OEB=Rt∠ ,根据圆的轴轴对称性,可得射线 EA 与 EB 重合,∴ 点 A 与点 B 重合,弧 AC 和弧 BC 重合,弧 AD 和弧 BD 重合.∴ EA=EB , AC= BC , AD=BD .⌒⌒⌒ ⌒思考:你能利用等腰三角形的性质,说明 OC 平分 AB 吗?垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.垂径定理的几何语言叙述 : CD 为直径, CDAB⊥(或 OCAB⊥) ∴ EA=EB , AC=BC , AD=BD . ⌒⌒⌒⌒结论 2 :ABOOCDE条件CD 为直径CDAB⊥CD 平分弧 ADBCD 平分弦 ABCD 平分弧 A B结论分一条弧成相等的两条弧的点 , 叫做这条弧的中点 .AB例例 11 ::已知已知 ABAB 如图,用直尺和圆规求作这条如图,用直尺和圆规求作这条弧的中点。弧的中点。⌒⌒E1. 连结 AB;⌒⌒2. 作 AB 的垂直平分线 CD, 交 AB 与点 E;作法 :∴ 点 E 就是所求 AB 的中点 .⌒⌒分析 : 要平分 AB, 只要画垂直于弦 AB 的直径 . 而这条直径应在弦 AB 的垂直平分线上 . 因此画 AB 的垂直平分线就能把 AB 平分 .⌒⌒变式: 求弧 AB 的四等分点.CDABEFGmn例例 22 ::一条排水管的截面如图所示。已知排水管的半一条排水管的截面如图所示。已知排水管的半径径 OB=10OB=10 ,水面宽,水面宽 AB=16AB=16 。求截面圆心。求截面圆心 OO 到水面的距到水面的距离。离。DC1088解 : 作 OC⊥AB 于 C, 由垂径定理得 :AC=BC=1/2AB=0.5×16=8 由勾股定理得...