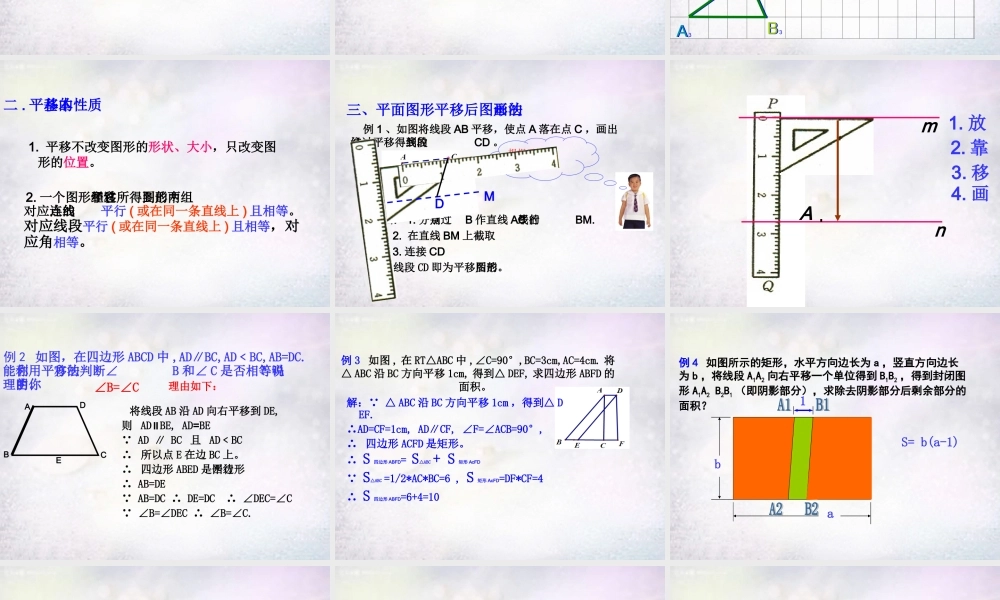
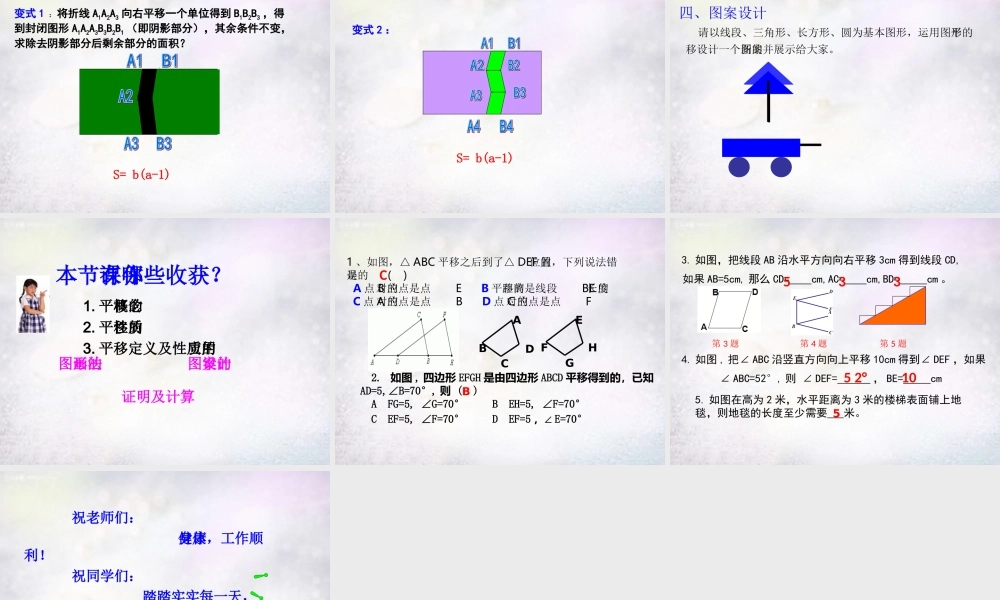
平移生活中你还见过其它物体平行移动的现象吗?AB1 、认识并欣赏平移在自然界和现实生活中的应用。2 、通过具体实例认识平移,探索并掌握它的基本性质。3 、运用平移的概念和基本性质,进行画图、证明、计算及图案设计。 一 . 平移概念在平面内 , 将一个图形沿某一个方向移动一定的距离,图形的这种变化叫做平移。(1) 平移的方向;决定平移的两个要素:(2) 平移的距离。把图中的△ ABC 向右平行移动不同的格数,画出所得到的△ A’B’C’.B1C1A1B3C3A3B2C2A2BCABCABCA二 . 平移的基本性质 2. 一个图形和它经过平移所得到的图形中,两组对应点的连线平行 ( 或在同一条直线上 ) 且相等。对应线段平行 ( 或在同一条直线上 ) 且相等,对应角相等。 1. 平移不改变图形的形状、大小,只改变图形的位置。三、平面图形平移后图形的画法 例 1 、如图将线段 AB 平移,使点 A 落在点 C ,画出经过这一平移得到的线段CD 。 画法: 1. 分别过点B 作直线 AC 的平行线BM. 2. 在直线 BM 上截取 3. 连接 CD 线段 CD 即为平移后的图形。根据平移的性质,还有别的画法吗?DMmnA1. 放2. 靠3. 移4. 画例 2 如图,在四边形 ABCD 中 ,AD∥BC,AD﹤BC,AB=DC.你能利用平移的方法判断∠B 和∠ C 是否相等吗?说明你的理由。ECBA D 将线段 AB 沿 AD 向右平移到 DE, 则 AD∥BE, AD=BE AD ∥ BC 且 AD﹤BC∴ 所以点 E 在边 BC 上。∴ 四边形 ABED 是平行四边形 ∴ AB=DE AB=DC ∴ DE=DC ∴ ∠DEC=∠C ∠B=∠DEC ∴ ∠B=∠C. ∠B=∠C理由如下: 例 3 如图 , 在 RT△ABC 中 ,∠C=90°,BC=3cm,AC=4cm. 将△ ABC 沿 BC 方向平移 1cm, 得到△ DEF, 求四边形 ABFD 的面积。 解: △ ABC 沿 BC 方向平移 1cm ,得到△ DEF.∴AD=CF=1cm, AD∥CF, ∠F=∠ACB=90°,∴ 四边形 ACFD 是矩形。 ∴ S 四边形 ABFD= S△ABC + S 矩形 AcFD S△ABC =1/2*AC*BC=6 , S 矩形 AcFD=DF*CF=4 ∴ S 四边形 ABFD=6+4=10 例 4 如图所示的矩形,水平方向边长为 a ,竖直方向边长为 b ,将线段 A1A2 向右平移一个单位得到 B1B2 ,得到封闭图形 A1A2 B2B1 (即阴影部分),求除去阴影部分后剩余部分的面积?S= b(a-1)ba1变式 1 :将折线 A1A2A3 向右平移一个单位得到 B1B2B3 ,得到封闭图形 A1A2A3B3B2B1 (即阴影部...