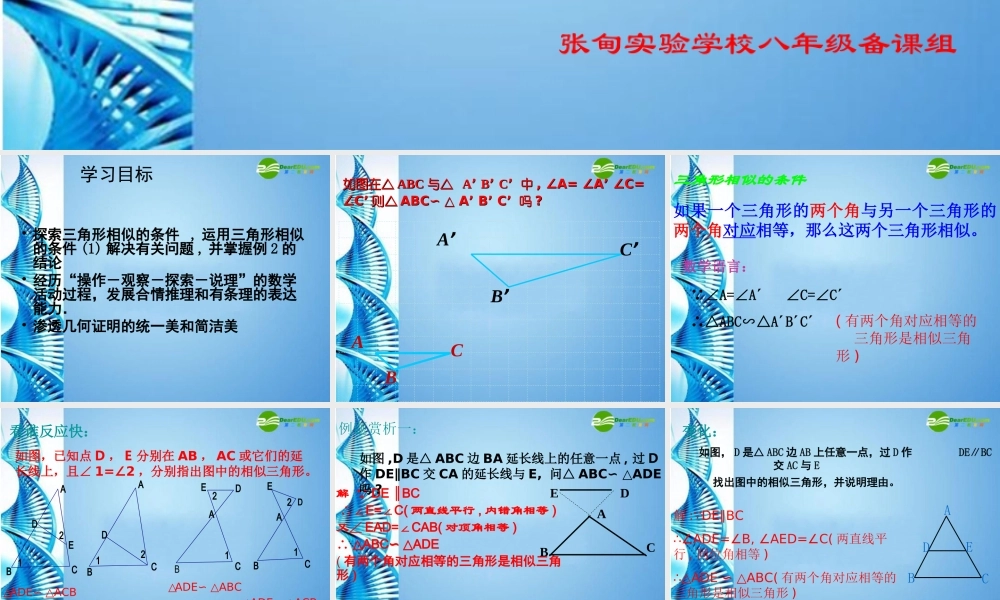
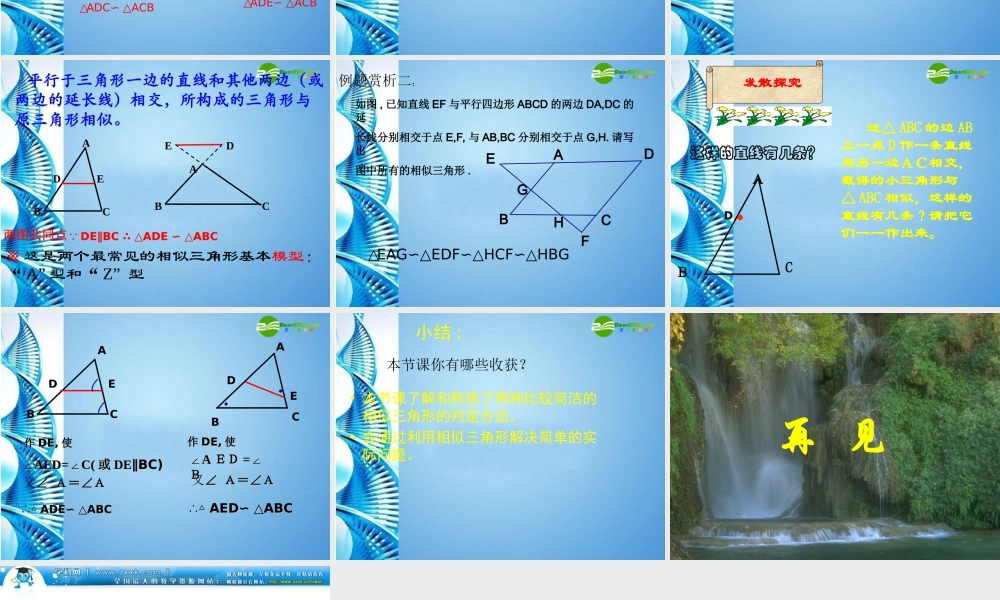
探索三角形相似的条件 (1)张甸实验学校八年级备课组学习目标• 探索三角形相似的条件 , 运用三角形相似的条件 (1) 解决有关问题 , 并掌握例 2 的结论• 经历“操作-观察-探索-说理”的数学活动过程,发展合情推理和有条理的表达能力.• 渗透几何证明的统一美和简洁美 如图在△ ABC 与△ A’ B’ C’ 中 , ∠A= ∠A’ ∠C= ∠C’ 则△ ABC∽ △ A’ B’ C’ 吗 ?如图在△ ABC 与△ A’ B’ C’ 中 , ∠A= ∠A’ ∠C= ∠C’ 则△ ABC∽ △ A’ B’ C’ 吗 ?ACBA’C’B’如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。三角形相似的条件∵∠A=∠A´ ∠C=∠C´∴△ABC∽△A´B´C´数学语言:( 有两个角对应相等的 三角形是相似三角形 )11122221DEAABDECCBCCBDDBEAA如图,已知点 D , E 分别在 AB , AC 或它们的延长线上,且∠ 1=∠2 ,分别指出图中的相似三角形。△ADE∽ △ACB△ADE∽ △ABC△ADC∽ △ACB△ADE∽ △ACB看谁反应快:• 解 ∵ DE BC∥• ∴∠E=C(∠两直线平行 , 内错角相等 )• 又∠ EAD=CAB(∠对顶角相等 )• ∴ △ABC ADE∽ △• ( 有两个角对应相等的三角形是相似三角形 )AEDBC如图 ,D 是△ ABC 边 BA 延长线上的任意一点 , 过 D作 DE∥BC 交 CA 的延长线与 E, 问△ ABC∽ △ADE吗 ?例题赏析一: 如图, D 是△ ABC 边 AB 上任意一点,过 D 作 DE∥BC交 AC 与 E 找出图中的相似三角形,并说明理由。 ABCDE解 :∵DE∥BC∴∠ADE=∠B, ∠AED=∠C( 两直线平行 , 同位角相等 )∴△ADE ∽ △ABC( 有两个角对应相等的三角形是相似三角形 )变化: 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。※ 这是两个最常见的相似三角形基本模型:“ A” 型和“ Z” 型ADEBCABEDC∵ DE∥BC ∴ △ADE ∽ △ABC两图共同点如图 , 已知直线 EF 与平行四边形 ABCD 的两边 DA,DC 的延长线分别相交于点 E,F, 与 AB,BC 分别相交于点 G,H. 请写出图中所有的相似三角形 . DAFHCGBE△EAG∽△EDF∽△HCF∽△HBG例题赏析二;发散探究 过△ ABC 的边 AB上一点 D 作一条直线与另一边AC相交,截得的小三角形与△ ABC 相似,这样的直线有几条?请把它们一一作出来。这样的直线有几条?CD ●ABBCADEEBCAD∴∴△ △ ADE∽ △ABCADE∽ △ABC∴∴△ △ AED∽ △ABCAED∽ △ABC∠∠AED=C(∠AED=C(∠或或 DEDE∥BC)∥BC)∠∠AA EDED =∠=∠BB作作 DE,DE, 使使作作 DE,DE, 使使又∠ A=∠A∠ A=∠A又∠ A=∠A∠ A=∠A小结 :• 本节课了解和熟悉了两种比较简洁的相似三角形的判定方法。• 会通过利用相似三角形解决简单的实际问题。本节课你有哪些收获?再 见