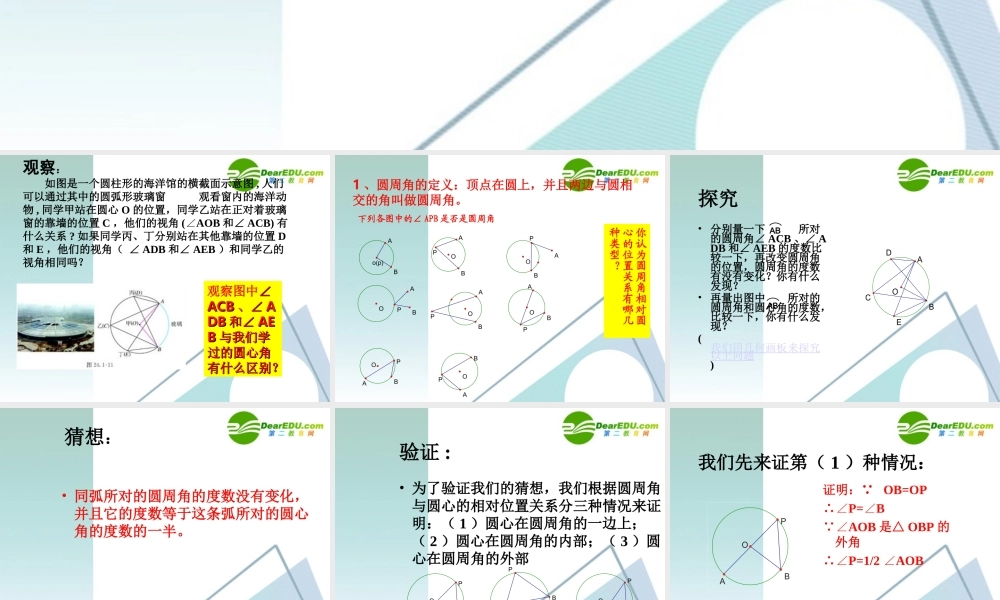
24.1.4 圆周角观察: 如图是一个圆柱形的海洋馆的横截面示意图 , 人们可以通过其中的圆弧形玻璃窗 观看窗内的海洋动物 , 同学甲站在圆心 O 的位置,同学乙站在正对着玻璃窗的靠墙的位置 C ,他们的视角 (AOB∠和∠ ACB) 有什么关系 ? 如果同学丙、丁分别站在其他靠墙的位置 D和 E ,他们的视角( ∠ ADB 和∠ AEB )和同学乙的视角相同吗?观察图中∠∠ACBACB 、∠、∠ AADBDB 和∠和∠ AEAEBB 与我们学与我们学过的圆心角过的圆心角有什么区别?有什么区别?1 、圆周角的定义:顶点在圆上,并且两边与圆相交的角叫做圆周角。下列各图中的∠ APB 是否是圆周角o(p)BOBPOAOPABOBOAOBOPAAPBAPPBAPAB你认为圆周角相对圆心的位置关系有哪几种类型?探究• 分别量一下 所对的圆周角∠ ACB 、∠ ADB 和∠ AEB 的度数比较一下,再改变圆周角的位置,圆周角的度数有没有变化?你有什么发现?• 再量出图中 所对的圆周角和圆心角的度数,比较一下,你有什么发现?(我们用几何画板来探究以上问题)ABABOBACDE猜想:• 同弧所对的圆周角的度数没有变化, 并且它的度数等于这条弧所对的圆心角的度数的一半。验证 :• 为了验证我们的猜想,我们根据圆周角与圆心的相对位置关系分三种情况来证明:( 1 )圆心在圆周角的一边上;( 2 )圆心在圆周角的内部;( 3 )圆心在圆周角的外部OBAPOBAPOPB我们先来证第( 1 )种情况:证明: OB=OP∴∠P=B∠ ∠AOB 是△ OBP 的外角∴∠P=1/2 AOB∠OBAP我们再来证明第( 2 )情况:连结 PO 并延长交⊙于 C由( 1 )可知:∠APC=1/2AOC∠∠BPC=1/2 BOC∠ ∴ ∠APC+ BPC=1/2∠( ∠AOC+ BOC∠)即∠ APB=1/2 AOB∠OAPBC最后我们来证明第( 3 )种情况:连结 PO 并延长交⊙ O 于C由( 1 )可知:∠APC=1/2AOC∠∠BPC=1/2 BOC∠ ∴ ∠BPC- APC =1/2∠( ∠ BOC- AOC ∠)即∠ APB=1/2 AOB∠OBAPc结论 :圆周角的定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。巩固练习:1 、圆周角的两个特征:( 1 ) , ( 2 ) 。 2 、在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的 。 3 、如图, AB 是⊙ O 的直径,∠ AOD 是圆心角, ∠ BCD 是圆周角,若∠ BCD=25° ,则∠ AOD= 。 OABCD顶点在圆上两边都与圆相交一半130°4 、如图, AB 是⊙ O 的...