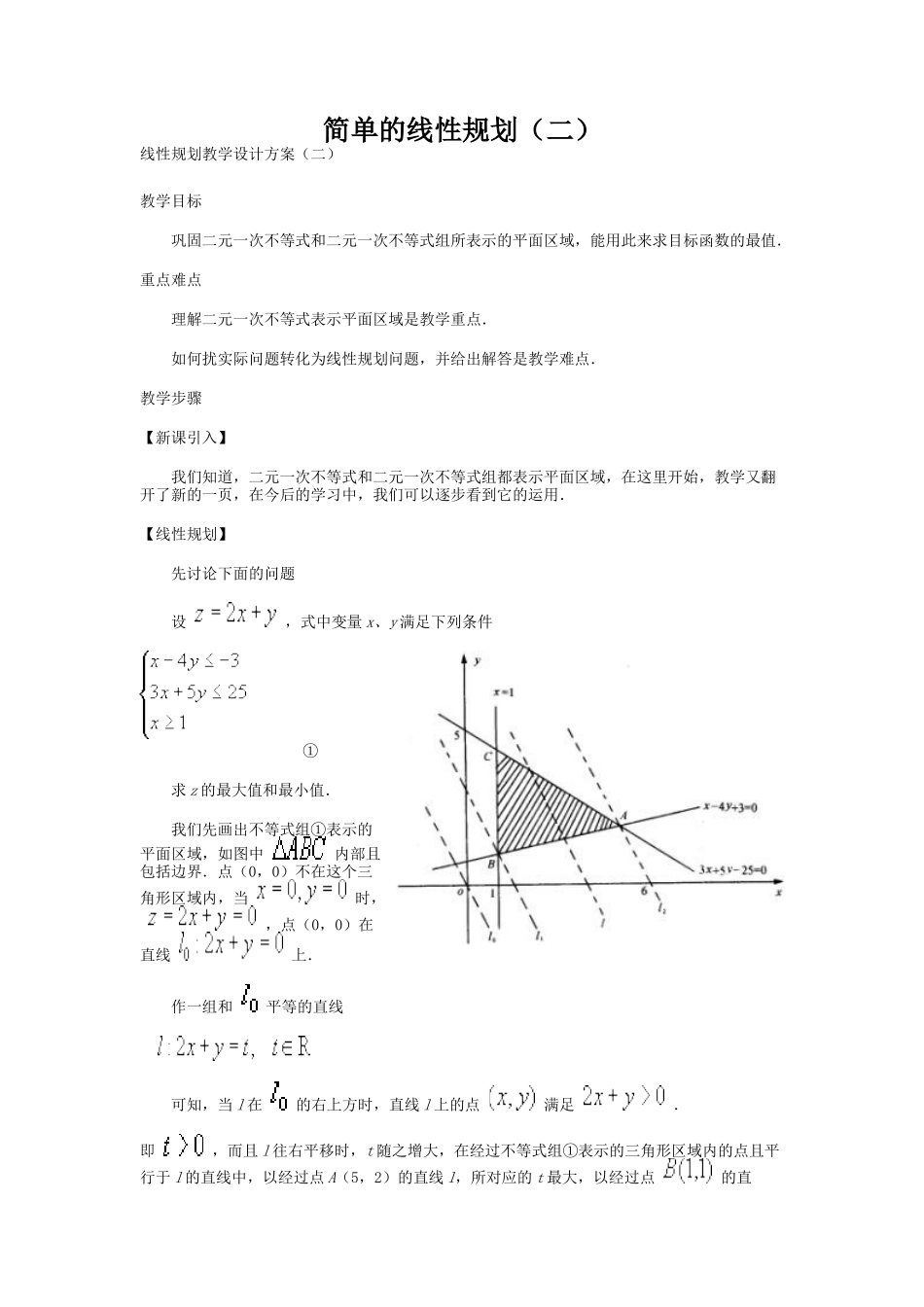
简单的线性规划(二)线性规划教学设计方案(二)教学目标 巩固二元一次不等式和二元一次不等式组所表示的平面区域,能用此来求目标函数的最值.重点难点 理解二元一次不等式表示平面区域是教学重点. 如何扰实际问题转化为线性规划问题,并给出解答是教学难点.教学步骤【新课引入】 我们知道,二元一次不等式和二元一次不等式组都表示平面区域,在这里开始,教学又翻开了新的一页,在今后的学习中,我们可以逐步看到它的运用.【线性规划】 先讨论下面的问题 设 ,式中变量 x、y 满足下列条件 ① 求 z 的最大值和最小值. 我们先画出不等式组①表示的平面区域,如图中 内部且包括边界.点(0,0)不在这个三角形区域内,当 时, ,点(0,0)在直线 上. 作一组和 平等的直线 可知,当 l 在 的右上方时,直线 l 上的点 满足 .即 ,而且 l 往右平移时,t 随之增大,在经过不等式组①表示的三角形区域内的点且平行于 l 的直线中,以经过点 A(5,2)的直线 l,所对应的 t 最大,以经过点 的直线 ,所对应的 t 最小,所以 在上述问题中,不等式组①是一组对变量 x、y 的约束条件,这组约束条件都是关于 x、y的一次不等式,所以又称线性约束条件. 是欲达到最大值或最小值所涉及的变量 x、y 的解析式,叫做目标函数,由于 又是 x、y 的解析式,所以又叫线性目标函数,上述问题就是求线性目标函数 在线性约束条件①下的最大值和最小值问题. 线性约束条件除了用一次不等式表示外,有时也有一次方程表示. 一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题,满足线性约束条件的解 叫做可行解,由所有可行解组成的集合叫做可行域,在上述问题中,可行域就是阴影部分表示的三角形区域,其中可行解(5,2)和(1,1)分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解.【应用举例】 例 1 解下列线性规划问题:求 的最大值和最小值,使式中的 x、y 满足约束条件 解:先作出可行域,见图中 表示的区域,且求得 . 作出直线 ,再将直线 平移,当 的平行线 过 B 点时,可使 达到最小值,当 的平行线 过 C 点时,可使 达到最大值. 通过这个例子讲清楚线性规划的步骤,即: 第一步:在平面直角坐标系中作出可行域; 第二步:在可行域内找出最优解所对应的点; 第三步:解方程的最优解,从而求出目标函数的最大值或最小值...