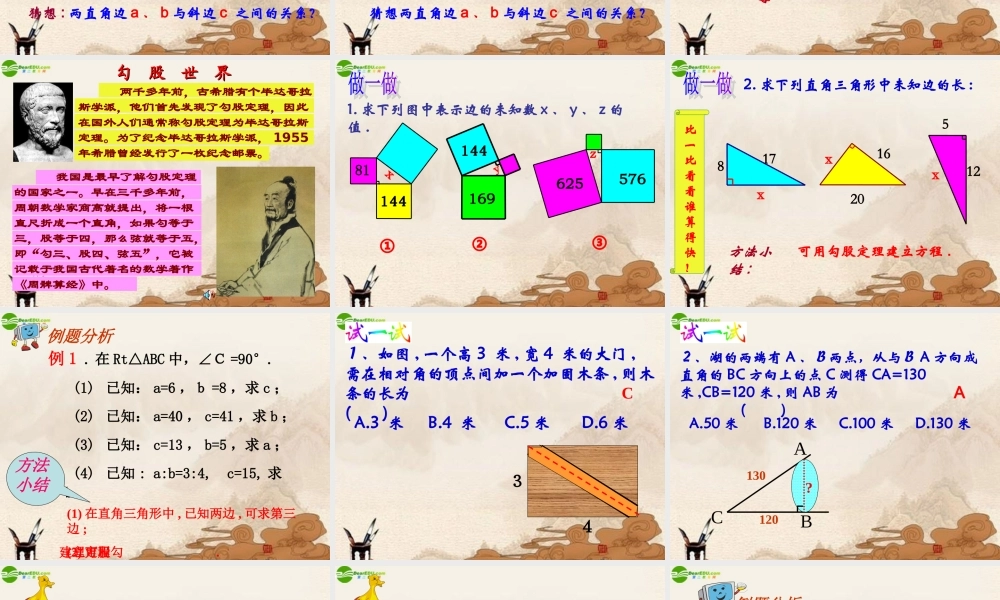
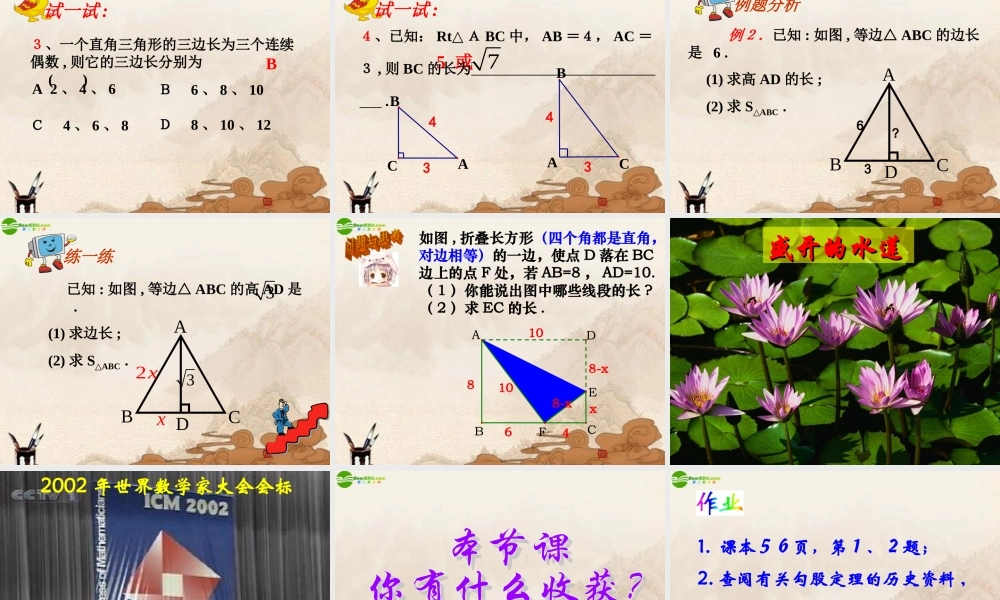
勾 股 定 勾 股 定 理理邮票赏邮票赏析析这是 1955 年希腊曾经发行的纪念一位数学家的邮票。 在方格纸上 ,画一个顶点都在格点上的直角三角形 ; 并分别以这个直角三角形的各边为一边向三角形外作正方形 , 计算以斜边为一边的正方形的面积 .PQCR如图,小方格的边长为 1.(1) 你能求出正方形 R 的面积吗?用了“补”的方法PQCR用了“割”的方法QPQRacbSP+SQ=SR 观察所得到的各组数据,你有什么发现?猜想 : 两直角边 a 、 b 与斜边 c 之间的关系?a2+b2=c2acbSP+SQ=SR 观察所得到的各组数据,你有什么发现?猜想两直角边 a 、 b 与斜边 c 之间的关系?a2+b2=c2┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方 .勾股弦 勾股定理 ( 毕达哥拉斯定理 ) 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派, 1955勾 股 世 界勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派, 1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。1. 求下列图中表示边的未知数 x 、 y 、 z 的值 .①81144xyz②③625576144169比一比看看谁算得快!2. 求下列直角三角形中未知边的长 :可用勾股定理建立方程 .方法小结 :8x171620x125x 例 1 . 在 Rt△ABC 中,∠C =90°. (1) 已知: a=6 ,b =8 ,求 c ; (2) 已知: a=40 , c=41 ,求 b ; (3) 已知: c=13 , b=5 ,求 a ; (4) 已知 : a:b=3:4, c=15, 求a 、 b.例题分析(1) 在直角三角形中 , 已知两边 , 可求第三边 ;(2) 可用勾股定理建立方程.方法小结1、如图 , 一个高 3 米 , 宽 4 米的大门 ,需在相对角的顶点间加一个加固木条 , ...