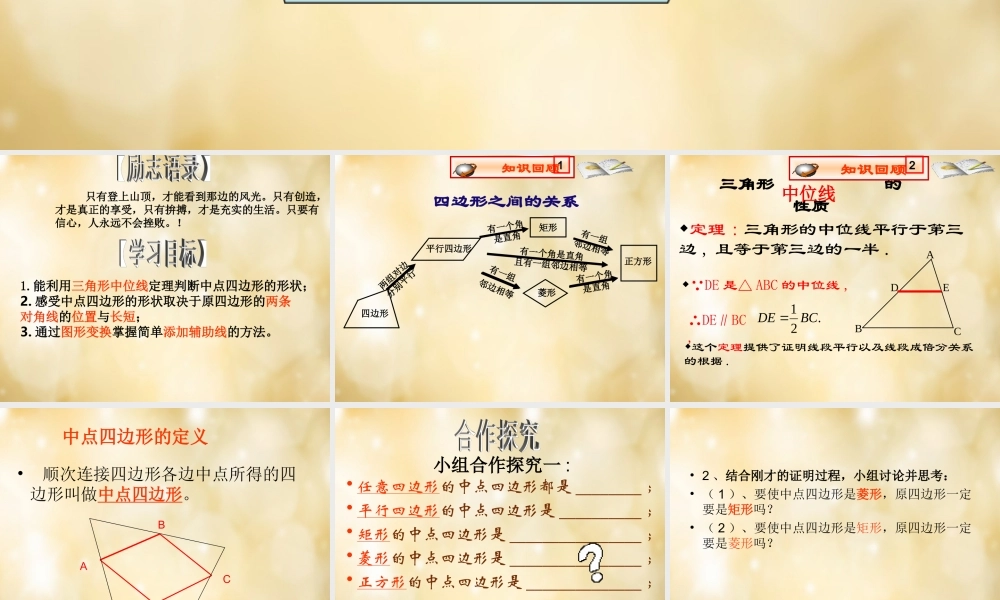
只有登上山顶,才能看到那边的风光。只有创造,才是真正的享受,只有拚搏,才是充实的生活。只要有信心,人永远不会挫败。! 1.能利用三角形中位线定理判断中点四边形的形状;2. 感受中点四边形的形状取决于原四边形的两条对角线的位置与长短;3. 通过图形变换掌握简单添加辅助线的方法。四边形之间的关系四边形平行四边形矩形正方形两组对边分别平行有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等 知识回顾11菱形菱形有一个角是直角且有一组邻边相等三角形 的性质定理 : 三角形的中位线平行于第三边 , 且等于第三边的一半 .这个定理提供了证明线段平行以及线段成倍分关系的根据 .∵DE 是△ ABC 的中位线 ,DEBCA.21 BCDE ∴DE∥BC, 知识回顾 22中位线ADCB中点四边形的定义• 顺次连接四边形各边中点所得的四边形叫做中点四边形。小组合作探究一 :• 任意四边形的中点四边形都是 ________ ;• 平行四边形的中点四边形是 __________ ;• 矩形的中点四边形是 ________________ ;• 菱形的中点四边形是 ________________ ;• 正方形的中点四边形是 ______________ ;• 2 、结合刚才的证明过程,小组讨论并思考:• ( 1 )、要使中点四边形是菱形,原四边形一定要是矩形吗?• ( 2 )、要使中点四边形是矩形,原四边形一定要是菱形吗?(3) 、如图:,点 E 、 F 、 G 、 H 分别是线段AB 、 BC 、 CD 、 AD 的中点,则四边形 EFGH 是什么图形?并说明理由。 CABDHEFG( 4 )、中点四边形的形状与原四边形的什么有密切关系?在凹四边形 ABCD 中O 点再三角形 ABC 的内部• 结论:• ( 1 )中点四边形的形状与原四边形的 有密切关系;• ( 2 )只要原四边形的两条对角线 _ _ ,就能使中点四边形是菱形;• ( 3 )只要原四边形的两条对角线 ,就能使中点四边形是矩形;• ( 4 )要使中点四边形是正方形,原四边形要符合的条件是 。对角线相等互相垂直相等且互相垂直探究点二、简单应用1 、请你设计一个中点四边形为正方形,但原四边形不是正方形的四边形。• 通过本节课的学习,你有什么收获?还有什么困惑?ABCDEFGH1 、如图:点 E 、 F 、 G 、 H 分别是线段 AB 、 BC 、 CD 、 AD 的中点,则四边形 EFGH 是什么图形?并说明理由。 •3. 如图,四边形 ABCD 中, AC = 6 , BD = 8 ,且 AC⊥BD 。顺次连结四边形 ABCD 各边中点,得到四边形;再顺次连结四边形各边中点,得到四边形……如此进行下去得到四边形。•( 1 )证明:四边形 是矩形;•( 2 )写出四边形 •和四边形 的面积;•( 3 )写出四边形 的面积;•( 4 )求四边形 的周长。