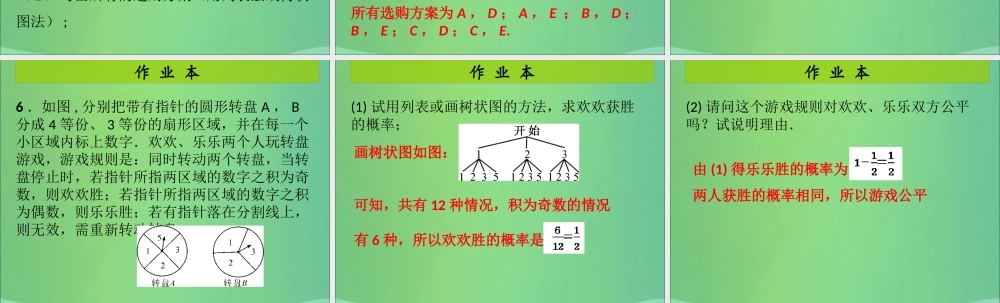
第 2 课时 用树状图或表格求概率（ 2 ）第三章 概率的进一步认识作 业 本一、选择或填空题（每题 10 分，共 40 分）1
袋子里有 4 个球，标有 2 ， 3 ， 4 ， 5 ，先抽取一个并记住，放回，然后再抽取一个，问抽取的两个球数字之和大于 6 的概率是 ( )C作 业 本2
有三张正面分别写有数字－ 1 ， 1 ， 2 的卡片，它们背面完全相同，现将这三张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为 a 的值，然后再从剩余的两张卡片中随机抽取一张，以其正面的数字作为 b 的值，则点 (a ，b) 在第二象限的概率是 ( )B作 业 本3
有两把不同的锁和三把钥匙，其中两把钥匙能打开同一把锁，第三把钥匙能打开另一把锁．任意取出一把钥匙去开任意一把锁，一次能打开锁的概率是 ．4 ．一个不透明的袋子中装有黑、白小球各两个，这些球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球都是白球的概率是 ．作 业 本二、解答题（每题 30 分，共 60 分）5 ．长城公司为希望小学捐赠甲、乙两种品牌的体育器材，甲品牌有 A ， B ， C 三种型号，乙品牌有 D ， E 两种型号，现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠
（ 1 ）写出所有的选购方案（用列表法或树状图法） ;作 业 本解：（ 1 ）列表如下：所有选购方案为 A ， D ； A ， E ； B ， D ；B ， E ； C ， D ； C ， E
甲品牌 乙品牌AＢＣD（Ａ，Ｄ） （Ｂ，Ｄ）（Ｃ，Ｄ）Ｅ（Ａ，Ｅ） （Ｂ，Ｅ）（Ｃ，Ｅ）作 业 本（ 2 ）如果在上述选购方案中，每种方案被选中的可能性相同，那么 A 型器材被选中的概率是多少
∵ 所有可能出现的结果共有 6 种，每种结果出现的可能性都相同， A 型器材被选中的结果有 2 种， ∴
