八年级数学下册(2.5 一元一次不等式与一次函数)课件3 (新版)北师大版 课件VIP免费

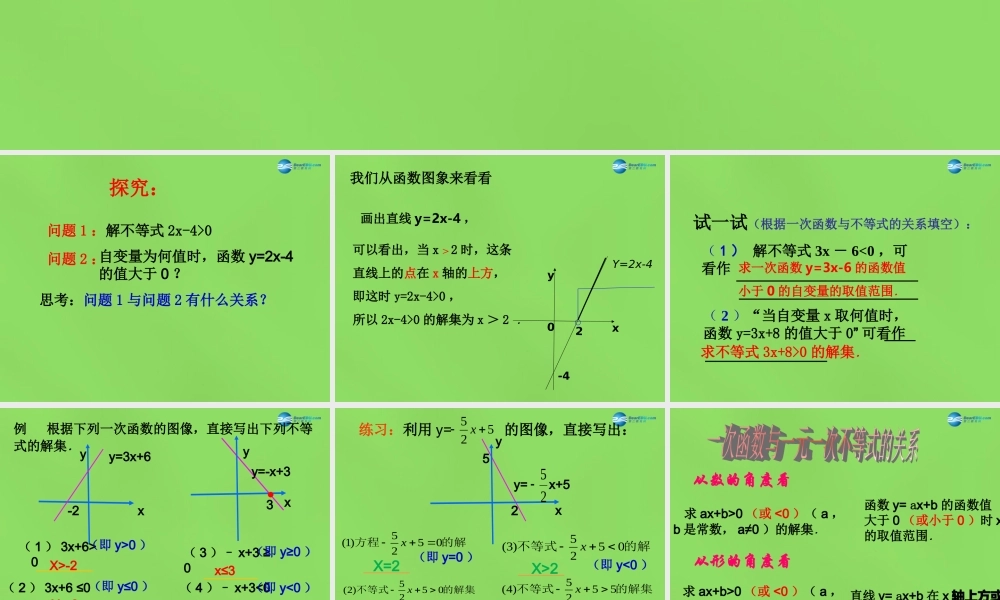
5 一元一次不等式与一次函数 5 一元一次不等式与一次函数 思考：问题 1 与问题 2 有什么关系？问题 2 ：自变量为何值时，函数 y=2x-4的值大于 0 ？问题 1 ：解不等式 2x-4>0探究：我们从函数图象来看看画出直线 y=2x-4 ，-42yx0Y=2x-4可以看出，当 x ＞2 时，这条直线上的点在 x 轴的上方，即这时 y=2x-4>0 ，所以 2x-4>0 的解集为 x ＞ 2 ．试一试（根据一次函数与不等式的关系填空）：求一次函数 y=3x-6 的函数值小于 0 的自变量的取值范围．求不等式 3x+8>0 的解集．（ 1 ） 解不等式 3x － 6<0 ，可看作（ 2 ）“当自变量 x 取何值时，函数 y=3x+8 的值大于 0” 可看作-2xy=3x+6y例 根据下列一次函数的图像，直接写出下列不等式的解集．（ 1 ） 3x+6>0（ 3 ）– x+3 ≥0xy3y=-x+3（ 2 ） 3x+6 ≤0X>-2（ 4 ）– x+3<0x≤3X≤-2x>3（即 y>0 ）（即 y≤0 ）（即 y<0 ）（即 y≥0 ）练习：利用 y= 的图像，直接写出：y525x25xy= x+525的解方程0525)1(x的解集不等式0525)2(x的解不等式0525)3(x的解集不等式5525)4(xX=2X<2X>2X<0（即 y=0 ）（即 y>0 ）（即 y<0 ）（即 y>5 ） 求 ax+b>0 （或 <0 ）（ a ， b 是常数， a≠0 ）的解集． 求 ax+b>0 （或 <0 ）（ a ， b 是常数， a≠0 ）的解集．函数 y= ax+b 的函数值大于 0 （或小于 0 ）时 x的取值范围．直线 y= ax+b 在 x 轴上方或下方时自变量的取值范围从数的角度看从形的角度看可以看出，当 x<2 时这条直线上的点在 x 轴的下方，解法一：化简得 3x-6<0 ，画出直线 y=3x-6 ，即这时 y=3x-6<0 ，所以不等式的解集为 x<2 ．用画函数图象的方法解不等式 5x+4<2x+10 ．yx-620Y=3x-6尝试：解法二：画出函数 y = 2x+10 y = 5x+4 图象． 从图中看出：当 x <2 时直线 y = 5x +4 在 y = 2x +10 的下方 即 5x+4 < 2x +10∴ 不等式 5x+4 < 2 x +10 的解集是x < 2 ．Y1=5x+4yx0Y2=2X+102-2当堂检测x>21 、如图是一次函数的图象，则关于 x 的方程的解为 ；关于 x 的不等式的解集为 ；的解集为 ．关于 x 的不等式x=2x<2)0( kbkxy0bkx0bkx0bkx当堂检测下方2 、若关于 x 的不等式 的解集为则一次函数当时，图象在时，图象在 x 轴 _____ ．x 轴 _________ ；当上方0bkxbkxy25x25x25x 1 、这节课我们学到了哪些知识？ 2 、我们是用哪些方法获得这些知识的？ 3 、你觉得还有什么问题需要继续讨论吗？回顾反思回顾反思 求一元一次不等式的解，可以看求一元一次不等式的解，可以看成某一个一次函数当自变量取何值时，函成某一个一次函数当自变量取何值时，函数的值大于零或等于零数的值大于零或等于零．