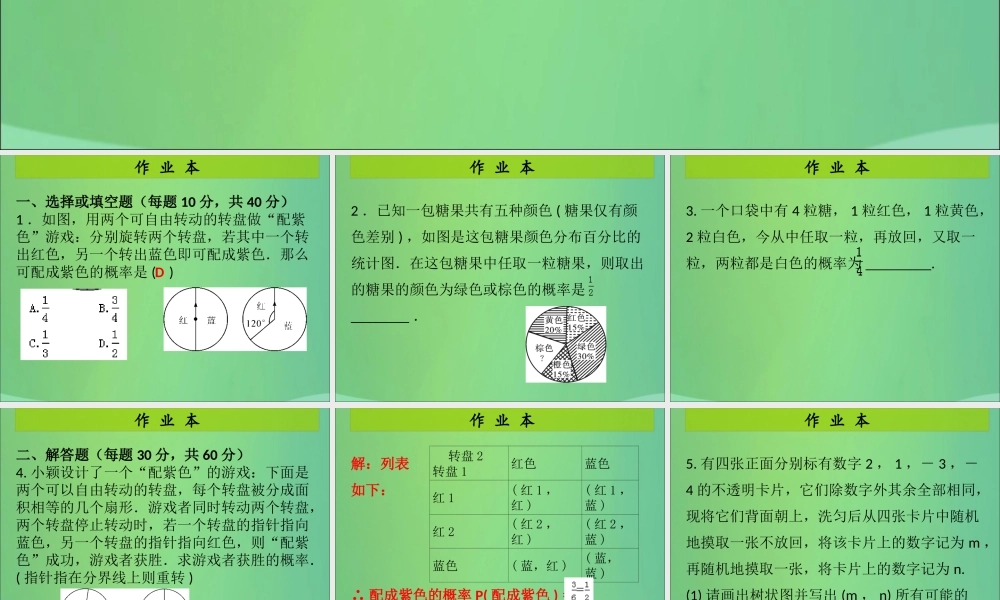
作 业 本第 3 课时 用树状图或表格求概率( 3 )第三章 概率的进一步认识作 业 本一、选择或填空题(每题 10 分,共 40 分)1 .如图,用两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色.那么可配成紫色的概率是 ( )D作 业 本2 .已知一包糖果共有五种颜色 ( 糖果仅有颜色差别 ) ,如图是这包糖果颜色分布百分比的统计图.在这包糖果中任取一粒糖果,则取出的糖果的颜色为绿色或棕色的概率是________ .作 业 本3. 一个口袋中有 4 粒糖, 1 粒红色, 1 粒黄色,2 粒白色,今从中任取一粒,再放回,又取一粒,两粒都是白色的概率为 _________.作 业 本二、解答题(每题 30 分,共 60 分)4. 小颖设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,两个转盘停止转动时,若一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则“配紫色”成功,游戏者获胜.求游戏者获胜的概率.( 指针指在分界线上则重转 )作 业 本解:列表如下:∴ 配成紫色的概率 P( 配成紫色 ) = ∴ 游戏者获胜的概率为 转盘 2转盘 1 红色蓝色红 1( 红 1 ,红 )( 红 1 ,蓝 )红 2( 红 2 ,红 )( 红 2 ,蓝 )蓝色( 蓝,红 )( 蓝,蓝 )作 业 本5. 有四张正面分别标有数字 2 , 1 ,- 3 ,-4 的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为 m ,再随机地摸取一张,将卡片上的数字记为 n.(1) 请画出树状图并写出 (m , n) 所有可能的结果;作 业 本解: (1) 画树状图:则 (m , n) 共有 12 种等可能的结果:(2 , 1) , (2 ,- 3) , (2 ,- 4) , (1 , 2) ,(1 ,- 3) , (1 ,- 4) , ( - 3 , 2) , ( - 3 ,1) ,( - 3 ,- 4) , ( - 4 , 2) , ( - 4 , 1) ,( - 4 ,- 3).作 业 本(2) 求所选出的 m , n 能使一次函数 y = mx+ n 的图象经过第二、三、四象限的概率.∵ 所选出的 m , n 能使一次函数 y = mx + n的图象经过第二、三、四象限的有 ( - 3 ,-4) ,( - 4 ,- 3) ,∴ 所选出的 m , n 能使一次函数 y = mx + n的图象经过第二、三、四象限的概率为